题目内容
【题目】如图,点A、B和线段CD都在数轴上,点A,C,D,B起始位置所表示的数分别为-2,0,3,12;线段CD沿数轴的正方向以每秒1个单位长度的速度运动,运动时间为1秒.
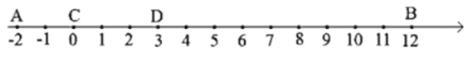
(1)当![]() =0秒时,AC的长为________,当
=0秒时,AC的长为________,当![]() =2秒时,AC的长为________;
=2秒时,AC的长为________;
(2)用含有![]() 的代数式表示AC的线段长为________;
的代数式表示AC的线段长为________;
(3)当![]() =__________秒时,AC-BD=5;当
=__________秒时,AC-BD=5;当![]() =___________秒时AC+BD=15;
=___________秒时AC+BD=15;
(4)若点A与线段CD同时出发沿数轴的正方向移动,点A的速度为每秒2个单位长度,在移动过程中,是否存在某一时刻使得AC=2BD,若存在,请直接求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)2,4;(2)![]() +2;(3)6,11;(4)16秒和
+2;(3)6,11;(4)16秒和![]() 秒
秒
【解析】
(1)依据A、C两点间的距离=|![]() -
-![]() |求解即可;
|求解即可;
(2)![]() 秒后点C运动的距离为
秒后点C运动的距离为![]() 个单位长度,从而点C表示的数;根据A、C两点间的距离=|
个单位长度,从而点C表示的数;根据A、C两点间的距离=|![]() -
-![]() |求解即可.
|求解即可.
(3)1秒后点C运动的距离为![]() 个单位长度,点D运动的距离为
个单位长度,点D运动的距离为![]() 个单位长度,从而可得到点A、点D表示的数;根据两点间的距离=|
个单位长度,从而可得到点A、点D表示的数;根据两点间的距离=|![]() -
-![]() |表示出AC、BD.根据AC-BD=5和AC+BD=15得到关于
|表示出AC、BD.根据AC-BD=5和AC+BD=15得到关于![]() 的含绝对值符号的一元次方程,分别解方程即可得出结论;
的含绝对值符号的一元次方程,分别解方程即可得出结论;
(4)假设能够相等,找出AC、BD,根据AC=2BD即可列出关于![]() 的含绝对值符号的一元一次方程,解方程即可得出结论.
的含绝对值符号的一元一次方程,解方程即可得出结论.
解:(1)当![]() =0秒时,AC=|-2-0|=|-2|=2;
=0秒时,AC=|-2-0|=|-2|=2;
当![]() =2秒时,移动后C表示的数为2,
=2秒时,移动后C表示的数为2,
∴AC=|-2-2|=4.
故答案为:2;4.
(2)点A表示的数为-2,点C表示的数为![]() ;
;
.AC=|-2-![]() |=
|=![]() +2.
+2.
故答案为![]() +2.
+2.
(3)∵![]() 秒后点C运动的距离为
秒后点C运动的距离为![]() 个单位长度,点D运动的距离为
个单位长度,点D运动的距离为![]() 个单位长度.
个单位长度.
∴C表示的数是![]() ,D表示的数是3+
,D表示的数是3+![]() ,
,
∴AC=![]() +2,BD=|12-(3+
+2,BD=|12-(3+![]() )|,
)|,
∵AC-BD=5,
∴![]() +2-|12-(
+2-|12-(![]() +3)|=5,
+3)|=5,
即![]() +2-|9-
+2-|9-![]() |=5,
|=5,
当![]() 时,t+2-(9-t)=5,
时,t+2-(9-t)=5,
解得:![]() =6;
=6;
当t>9时,t+2+(9-t)=5,此时无解;
∴t=6.
∴当![]() =6秒时AC-BD=5;
=6秒时AC-BD=5;
∵AC+BD=15,
∴![]() +2+|12-(
+2+|12-(![]() +3) |=15,
+3) |=15,
即![]() +2+|9-
+2+|9-![]() |=15
|=15
当![]() 时,t+2+(9-t)=15,此时无解;
时,t+2+(9-t)=15,此时无解;
当t>9时,t+2-(9-t)=15,解得t=11;
当![]() =11秒时AC+BD=15,
=11秒时AC+BD=15,
故答案为6,11;
(4)假设能相等,则点A表示的数为2![]() -2,C表示的数为
-2,C表示的数为![]() ,D表示的数为
,D表示的数为![]() +3,B表示的数为12,
+3,B表示的数为12,
∴AC=|2![]() -2-
-2-![]() |=|
|=|![]() -2|,BD=|
-2|,BD=|![]() +3-12|=|
+3-12|=|![]() -9|,
-9|,
∵AC=2BD,
∴|![]() -2|=2|
-2|=2|![]() -9|,
-9|,
∴|![]() -2|=|2
-2|=|2![]() -18|
-18|
解得:![]() =16,
=16,![]() .
.
故在运动的过程中使得AC=2BD,此时运动的时间为16秒和![]() 秒.
秒.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图
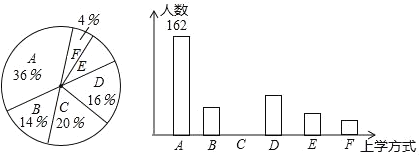
根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.