题目内容
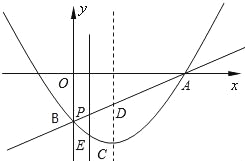
【题目】已知:如图1,点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.
(1)求证:AE=AF;
(2)如图2,若∠BAC=60°,△ABD的面积为4,连接AD交EF于M,连接BM、CM,在不添加任何辅助线的情况下,请直接写出图中所有面积为1的三角形.
【答案】
(1)
证明:∵DE⊥AC,DF⊥AB,
∴∠DFB=∠DEC=90°,
在RT△DBF和RT△DCE中,
![]() ,
,
∴△DBF≌△DCE,
∴∠B=∠C,
∴AB=AC,∵BF=CE,
∴AF=AE.
(2)
解:∵AF=AE,
∠AFE=∠AEF,
∵∠A+2∠AFE=180°,∠A+2∠B=180°,
∴∠AFE=∠B,
∴EF∥BC,
∵BD=DC,
∴S△BDF=S△BDM=S△CDM=S△CDE,
设BD=a,∵∠BAC=60°,AB=AC,
∴△ABC是等边三角形,
∴∠ABC=60°,AD= ![]() BD=
BD= ![]() a,
a,
∴S△ABD= ![]() a
a ![]() a=4,
a=4,
∴a2= ![]()
∴S△BDF= ![]() BFDF=
BFDF= ![]()
![]() a
a ![]() a=
a= ![]() a2=1,
a2=1,
∴S△BDF=S△BDM=S△CDM=S△CDE=1
【解析】(1)由△DBF≌△DCE得∠B=∠C,根据等角对等边得AB=AC,由此即可证明.(2)首先证明EF∥BC,得S△BDF=S△BDM=S△CDM=S△CDE , 设BD=a,根据S△ABD=4得出a2= ![]() ,再求出S△BDF=1,由此即可解决问题.
,再求出S△BDF=1,由此即可解决问题.

练习册系列答案
相关题目