题目内容
【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;
②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
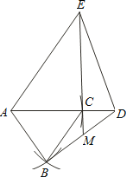
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺
规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).

【答案】(1)①BD=CE,理由见解析②180°-2α(2)BD=kCE,![]() α(3)
α(3)![]()
【解析】解:(1)如图1。
①BD=CE,理由如下:
∵AD=AE,∠ADE=α,∴∠AED=∠ADE=α,。∴∠DAE=180°-2∠ADE=180°-2α。同理可得:∠BAC=180°-2α。∴∠DAE=∠BAC。
∴∠DAE+∠BAE=∠BAC+∠BAE,即:∠BAD=∠CAE。
在△ABD与△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS)。∴BD=CE。
②∵△ABD≌△ACE,∴∠BDA=∠CEA。
∵∠BMC=∠MCD+∠MDC,∴∠BMC=∠MCD+∠CEA=∠DAE=180°-2α。
(2)如图2,BD=kCE,![]() α。
α。
(3)作图如下:
![]() 。
。
(1)①先根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC,则∠BAD=∠CAE,再根据SAS证明△ABD≌△ACE,从而得出BD=CE。
②先由全等三角形的对应角相等得出∠BDA=∠CEA,再根据三角形的外角性质即可得出
∠BMC=∠DAE=180°-2α。
(2)∵AD=ED,∠ADE=α,∴∠DAE=![]() 。
。
同理可得:∠BAC=![]() 。
。
∴∠DAE=∠BAC。
∴∠DAE+∠BAE=∠BAC+∠BAE,即:∠BAD=∠CAE。
∵AB=kAC,AD=kAE,∴AB:AC=AD:AE=k。
在△ABD与△ACE中,∵AB:AC=AD:AE=k,∠BDA=∠CEA,∴△ABD∽△ACE。
∴BD:CE=AB:AC=AD:AE=k,∠BDA=∠CEA。∴BD=kCE。
∵∠BMC=∠MCD+∠MDC,∴∠BMC=∠MCD+∠CEA=∠DAE=![]() 。
。
(3)先在备用图中利用SSS作出旋转后的图形,再根据等腰三角形等角对等边的性质及三角形内角和定理得出∠DAE=∠BAC=![]() ,由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,从而证出△ABD∽△ACE,得出∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=
,由AB=kAC,AD=kAE,得出AB:AC=AD:AE=k,从而证出△ABD∽△ACE,得出∠BDA=∠CEA,然后根据三角形的外角性质即可得出∠BMC=![]() :
:
∵AD=ED,∠ADE=α,∴∠DAE=∠AED=![]() 。
。
同理可得:∠BAC=![]() 。
。
∴∠DAE=∠BAC,即∠BAD=∠CAE。
∵AB=kAC,AD=kAE,∴AB:AC=AD:AE=k。
在△ABD与△ACE中,∵AB:AC=AD:AE=k,∠BAD=∠CAE,∴△ABD∽△ACE。
∴∠BDA=∠
∵∠BMC=∠MCD+∠MDC,∠MCD=∠CED+∠ADE=∠CED+α,
∴∠BMC=∠CED+α+∠CEA=∠AED+α=![]() +α=
+α=![]() 。
。