题目内容
已知抛物线 ,
,
【小题1】若n="-1," 求该抛物线与 轴的交点坐标;
轴的交点坐标;
【小题2】当 时,抛物线与
时,抛物线与 轴有且只有一个公共点,求n的取值范围.
轴有且只有一个公共点,求n的取值范围.
【小题1】解:(1)当n=-1时,抛物线为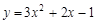 ,
,
方程 的两个根为:x=-1或x=
的两个根为:x=-1或x=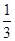 .
.
∴该抛物线与 轴公共点的坐标是
轴公共点的坐标是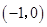 和
和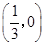 .
.
【小题2】∵抛物线与 轴有公共点.
轴有公共点.
∴对于方程 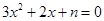
 ,判别式△=4-12n≥0,∴n≤
,判别式△=4-12n≥0,∴n≤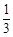 .
.
①当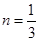 时,由方程
时,由方程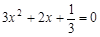 ,解得
,解得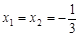 .
.
此时抛物线为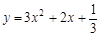 与
与 轴只有一个公共点
轴只有一个公共点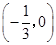 .
.
②当n<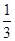 时,
时,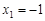 时,
时,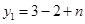 =1+n
=1+n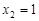 时,
时,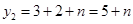
由已知 时,该抛物线与
时,该抛物线与 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为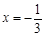 ,
,
应有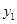 ≤0,且
≤0,且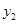 >0 即1+n≤0,且5+n>0
>0 即1+n≤0,且5+n>0
解得:-5<n≤-1.
综合①、②得n的取值范围是: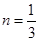 或-5<n≤-1.
或-5<n≤-1.
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, ,求该抛物线与
,求该抛物线与 轴公共点的坐标;
轴公共点的坐标;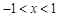 时,抛物线与
时,抛物线与 的取值范围;
的取值范围; ,且
,且 时,对应的
时,对应的 ;
; 时,对应的
时,对应的 ,试判断当
,试判断当 时,抛物线与
时,抛物线与 。【小题1】<1>求抛物线顶点M的坐标;
。【小题1】<1>求抛物线顶点M的坐标; .
. .
.