题目内容
已知抛物线
。【小题1】<1>求抛物线顶点M的坐标；
【小题2】 <2>若抛物线与x轴的交点分别为点A、B（点A在点B的左边），与y轴交于点C，点N为线段BM上的一点，过点N作x轴的垂线，垂足为点Q．当点N在线段BM上运动时（点N不与点B，点M重合），设NQ的长为t，四边形NQAC的面积为S，求S与t之间的函数关系式及自变量t的取值范围；
【小题3】 <3>在对称轴右侧的抛物线上是否存在点P，使△PAC为直角三角形?若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
【小题1】（1）顶点坐标
【小题2】（2）求与坐标轴的交点坐标ABC…………………………………2’
令y=-t代入BM直线解析式。…………………………………3’
将面积分割求。
。。。。。。。。。。。。。。。各一分5
【小题3】（3）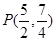
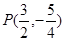。。。。。。。。。。。。各一分8
解析
练习册系列答案
相关题目
，
，
，求该抛物线与
轴公共点的坐标；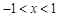
时，抛物线与
的取值范围；
，且
时，对应的
；
时，对应的
，试判断当
时，抛物线与
，
轴的交点坐标；
时，抛物线与
．
．