ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΘ®±ΨΧβ¬ζΖ÷![]() Ζ÷Θ©
Ζ÷Θ©
Θ®![]() Θ©ΓΨΈ ΧβΓΩ»γΆΦ
Θ©ΓΨΈ ΧβΓΩ»γΆΦ![]() Θ§Βψ
Θ§Βψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() Άβ“ΜΕ·ΒψΘ§«“
Άβ“ΜΕ·ΒψΘ§«“![]() Θ§
Θ§ ![]() Θ°Β±Βψ
Θ°Β±Βψ![]() ΈΜ”Ύ__________ ±œΏΕΈ
ΈΜ”Ύ__________ ±œΏΕΈ![]() ΒΡ≥Λ»ΓΒΟΉν¥σ÷ΒΘ§«“Ήν¥σ÷ΒΈΣ__________Θ®”ΟΚ§
ΒΡ≥Λ»ΓΒΟΉν¥σ÷ΒΘ§«“Ήν¥σ÷ΒΈΣ__________Θ®”ΟΚ§![]() ΓΔ
ΓΔ![]() ΒΡ ΫΉ”±μ ΨΘ©Θ°
ΒΡ ΫΉ”±μ ΨΘ©Θ°
Θ®![]() Θ©ΓΨ”Π”ΟΓΩΒψ
Θ©ΓΨ”Π”ΟΓΩΒψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ≥ΐΆβ“ΜΕ·ΒψΘ§«“
≥ΐΆβ“ΜΕ·ΒψΘ§«“![]() Θ§
Θ§ ![]() Θ°»γΆΦ
Θ°»γΆΦ![]() Υυ ΨΘ§Ζ÷±π“‘
Υυ ΨΘ§Ζ÷±π“‘![]() ΓΔ
ΓΔ![]() ΈΣ±ΏΘ§
ΈΣ±ΏΘ§
ΉςΒ»±Ώ»ΐΫ«–Έ![]() ΚΆΒ»±Ώ»ΐΫ«–Έ
ΚΆΒ»±Ώ»ΐΫ«–Έ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ°
Θ°
ΔΌ«κ’“≥ωΆΦ÷–”κ![]() œύΒ»ΒΡœΏΕΈΘ§≤ΔΥΒΟςάμ”…Θ°
œύΒ»ΒΡœΏΕΈΘ§≤ΔΥΒΟςάμ”…Θ°
ΔΎ÷±Ϋ”–¥≥ωœΏΕΈ![]() ≥ΛΒΡΉν¥σ÷ΒΘ°
≥ΛΒΡΉν¥σ÷ΒΘ°
Θ®![]() Θ©ΓΨΆΊ’ΙΓΩ»γΆΦ
Θ©ΓΨΆΊ’ΙΓΩ»γΆΦ![]() Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ
Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ
![]() Άβ“ΜΕ·ΒψΘ§«“
Άβ“ΜΕ·ΒψΘ§«“![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ°«κ÷±Ϋ”–¥≥ωœΏΕΈ
Θ°«κ÷±Ϋ”–¥≥ωœΏΕΈ![]() ≥ΛΒΡΉν¥σ÷ΒΦΑ¥Υ ±Βψ
≥ΛΒΡΉν¥σ÷ΒΦΑ¥Υ ±Βψ![]() ΒΡΉχ±ξΘ°
ΒΡΉχ±ξΘ°




ΓΨ¥πΑΗΓΩΘ®![]() Θ©
Θ©![]() ―”≥ΛœΏ…œΘ§
―”≥ΛœΏ…œΘ§ ![]() ΘΜΘ®
ΘΜΘ®![]() Θ©ΔΌ
Θ©ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() Θ®
Θ®![]() Θ©
Θ©![]() ΘΜ
ΘΜ ![]()
ΓΨΫβΈωΓΩΘ®![]() Θ©Β±»ΐΒψ≤ΜΙ≤œΏ ±Θ§»ΐΫ«–ΈΝΫ±Ώ÷°ΚΆ¥σ”ΎΒΎ»ΐ±ΏΘ§Φ¥
Θ©Β±»ΐΒψ≤ΜΙ≤œΏ ±Θ§»ΐΫ«–ΈΝΫ±Ώ÷°ΚΆ¥σ”ΎΒΎ»ΐ±ΏΘ§Φ¥![]() ΘΜ
ΘΜ
Β±![]() ‘Ύ
‘Ύ![]() ―”≥ΛœΏ…œ ±Θ§
―”≥ΛœΏ…œ ±Θ§ ![]() ΘΜ
ΘΜ
Β±![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ ±Θ§
…œ ±Θ§ ![]() Θ°
Θ°
Ι Β±![]() ‘Ύ
‘Ύ![]() ―”≥ΛœΏ…œ ±Θ§
―”≥ΛœΏ…œ ±Θ§ ![]() »ΓΒΟΉν¥σ÷ΒΘ§«“ΈΣ
»ΓΒΟΉν¥σ÷ΒΘ§«“ΈΣ![]() Θ°
Θ°
Θ®![]() Θ©ΔΌ“άΧβ“βΒΟ
Θ©ΔΌ“άΧβ“βΒΟ![]() Θ§
Θ§ ![]() Θ§άϊ”ΟΒ»±Ώ»ΐΫ«–ΈΟΩΗωΫ«ΕΦ «
Θ§άϊ”ΟΒ»±Ώ»ΐΫ«–ΈΟΩΗωΫ«ΕΦ «![]() ΚΆΫ«ΒΡΙΊœΒΒΟ
ΚΆΫ«ΒΡΙΊœΒΒΟ![]() Θ§
Θ§
ΉνΚσΗυΨί±ΏΫ«±ΏΕ®άμ÷ΛΟς![]() Γ’
Γ’![]() Θ§
Θ§
¥”ΕχΆΤ≥ω![]() Θ°
Θ°
ΔΎ“ρΈΣ![]() Θ§Υυ“‘œΏΕΈ
Θ§Υυ“‘œΏΕΈ![]() ΒΡΉν¥σ÷ΒΦ¥
ΒΡΉν¥σ÷ΒΦ¥![]() ΒΡΉν¥σ÷ΒΘ°
ΒΡΉν¥σ÷ΒΘ°
ΗυΨί»ΐΫ«–ΈΝΫ±Ώ÷°ΚΆ¥σ”ΎΒΎ»ΐ±ΏΘ§Υυ“‘![]() Ήν¥σ ±Φ¥
Ήν¥σ ±Φ¥![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() »ΐΒψΙ≤œΏΘ§
»ΐΒψΙ≤œΏΘ§
ΒΟΒΫ![]() ΒΡΉν¥σ÷ΒΈΣ
ΒΡΉν¥σ÷ΒΈΣ![]() Θ§
Θ§
Ι ![]() ΒΡΉν¥σ÷ΒΈΣ
ΒΡΉν¥σ÷ΒΈΣ![]() Θ°
Θ°
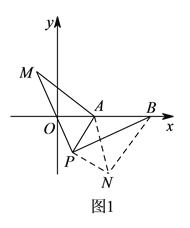
Θ®![]() Θ©»γΆΦ1Θ§“‘Βψ
Θ©»γΆΦ1Θ§“‘Βψ![]() ΈΣ‘≤–ΡΘ§
ΈΣ‘≤–ΡΘ§ ![]() ΈΣΑκΨΕΉςΜΓΘ§ΫΜ“‘Βψ
ΈΣΑκΨΕΉςΜΓΘ§ΫΜ“‘Βψ![]() ΈΣ‘≤–ΡΘ§
ΈΣ‘≤–ΡΘ§
![]() ΈΣΑκΨΕΉςΒΡΜΓ”ΎΒψ
ΈΣΑκΨΕΉςΒΡΜΓ”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() Θ§‘ρ
Θ§‘ρ![]() Θ°
Θ°
‘Ύ![]() ΚΆ
ΚΆ![]() ÷–Θ§
÷–Θ§
 Θ§
Θ§
Υυ“‘![]() Γ’
Γ’![]() Θ§
Θ§
Υυ“‘![]() Θ§”÷“ρΈΣ
Θ§”÷“ρΈΣ![]() Θ§
Θ§
Υυ“‘![]() Θ§Φ¥
Θ§Φ¥![]() Θ°
Θ°
”…Θ®![]() Θ©Ω…÷ΣΘ§Β±Βψ
Θ©Ω…÷ΣΘ§Β±Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œ ±Θ§
ΒΡ―”≥ΛœΏ…œ ±Θ§ ![]() »ΓΒΟΉν¥σ÷ΒΘ§
»ΓΒΟΉν¥σ÷ΒΘ§
”÷“ρΈΣ![]() Θ§Υυ“‘¥Υ ±
Θ§Υυ“‘¥Υ ±![]() »ΓΒΟΉν¥σ÷ΒΘ°
»ΓΒΟΉν¥σ÷ΒΘ°
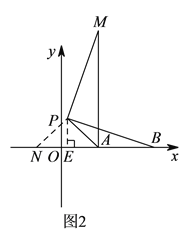
»γΆΦ2Θ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œ ±Θ§ΙΐΒψ
ΒΡ―”≥ΛœΏ…œ ±Θ§ΙΐΒψ![]() Ής
Ής![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ°
Θ°
‘Ύ![]() ÷–Θ§”…Ι¥Ι…Ε®άμΒΟ
÷–Θ§”…Ι¥Ι…Ε®άμΒΟ
![]() Θ§
Θ§
Υυ“‘![]() Θ°
Θ°
“ρΈΣ![]() Θ§
Θ§ ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
«Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
”÷“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§
Θ§
”÷“ρΈΣΒψ![]() Θ§
Θ§
Υυ“‘![]() Θ§
Θ§
Υυ“‘Βψ![]() Ήχ±ξΈΣ
Ήχ±ξΈΣ![]() Θ°
Θ°

 ≥ε¥Χ100Ζ÷ΒΞ‘Σ”≈Μ·ΝΖΩΦΨμœΒΝ–¥πΑΗ
≥ε¥Χ100Ζ÷ΒΞ‘Σ”≈Μ·ΝΖΩΦΨμœΒΝ–¥πΑΗ