题目内容
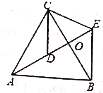
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一条直线上,BC和AE相交于点O,连接BE,若∠CAB=∠CBA=∠CDE=∠CED=50°。
(1)求证:AD=BE;
(2)求∠AEB。
【答案】(1)详见解析;(2)∠AEB=80°.
【解析】
(1)欲证明AD=BE,只要证明△ACD≌△BCE(SAS)即可.
(2)利用:“8字型”可以证明∠OEB=∠ACO,即可解决问题.
(1)证明:
∵∠CAB=∠CBA=∠CDE=∠CED=50°,
∴CA=CB,CD=CE,∠ACB=∠DCE=80°,∴∠ACD=∠BCE,
在△ACD和△BCE中,
 ,∴△ACD≌△BCE(SAS),
,∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:∵△ACD≌△BCE,∴∠CAD=∠CBE,
∵∠COA=∠BOE,∴∠ACO=∠BEO=80°,
∴∠AEB=80°.

练习册系列答案
相关题目
【题目】如图,在△ABC中, ![]() ,
, ![]() °,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至
°,点D是线段BC上的动点,将线段AD绕点A顺时针旋转50°至![]() ,连接
,连接![]() .已知AB
.已知AB![]() 2cm,设BD为x cm,B
2cm,设BD为x cm,B![]() 为y cm.
为y cm.

小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整.(说明:解答中所填数值均保留一位小数)
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | 2.3 |
| 1.7 | 1.3 | 1.1 | 0.7 | 0.9 | 1.1 |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:
线段![]() 的长度的最小值约为__________
的长度的最小值约为__________ ![]() ;
;
若![]()
![]() ,则
,则![]() 的长度x的取值范围是_____________.
的长度x的取值范围是_____________.