题目内容
【题目】已知,△ABC中,∠ACB=90°,AC=BC,点D为BC边上的一点.
(1)以点C为旋转中心,将△ACD逆时针旋转90°,得到△BCE,请你画出旋转后的图形;
(2)延长AD交BE于点F,求证:AF⊥BE;
(3)若AC=![]() ,BF=1,连接CF,则CF的长度为______.
,BF=1,连接CF,则CF的长度为______.

【答案】(1)答案见解析;(2)答案见解析;(3)![]() .
.
【解析】试题分析:(1)根据题意补全图形;
(2)由旋转的性质得到∠CBE=∠CAD,∠BCE=∠ACD=90°,进而得到∠CAD+∠E=90°,即可的得到结论;
(3)易证△ADC∽△BDF,△ADB∽△CDF,由相似三角形的性质即可得到结论.
试题解析:解:(1)补全图形如下:
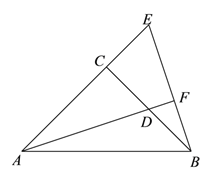
(2)证明:∵ΔCBE由ΔCAD旋转得到,∴ΔCBE≌ΔCAD,∴∠CBE=∠CAD,∠BCE=∠ACD=90°,∴∠CBE+∠E=∠CAD+∠E,∴∠BCE=∠AFE=90°,∴AF⊥BE.
(3)∵∠ACB=∠DFB=90°,∠CDA=∠FDB,∴△ADC∽△BDF,∴ ![]() ,∴
,∴![]() .∵∠ADB=∠CDF,∴△ADB∽△CDF,∴
.∵∠ADB=∠CDF,∴△ADB∽△CDF,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴CF=
,∴CF=![]() .
.


练习册系列答案
相关题目