题目内容
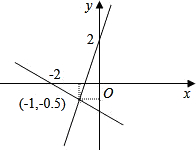写出如图所示的直线解析式分析：这两条直线分别经过点（0，2），（-1，-0.5）和（-2，0），（-1，-0.5），根据待定系数法就可以求出两直线的解析式，并可以求出函数与x轴的交点坐标，就可以得到两条条直线与坐标轴围成的三角形的面积．
解答：解：将点（0，2），（-1，-0.5）代入直线解析式y=kx+b，
解得k=2.5，b=2，
故直线解析式为y=2.5x+2；
将点（-2，0），（-1，-0.5）代入直线解析式y=kx+b，
解得k=-0.5，b=-1，
故直线解析式为y=-0.5x-1．
图中两条直线与两坐标轴所围成的面积是
．
解得k=2.5，b=2，
故直线解析式为y=2.5x+2；
将点（-2，0），（-1，-0.5）代入直线解析式y=kx+b，
解得k=-0.5，b=-1，
故直线解析式为y=-0.5x-1．
图中两条直线与两坐标轴所围成的面积是
| 2 |
| 5 |
点评：利用待定系数法求函数解析式是求解析式最常用的方法．
练习册系列答案
相关题目
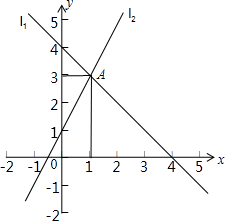已知如图所示，直线L1，L2相交于A点，请根据图象写出以交点坐标为解的二元一次方程组，并求出它的解．
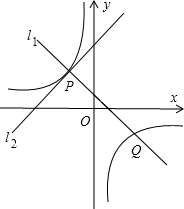线
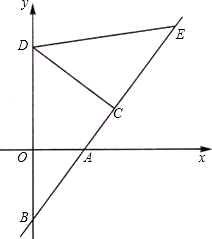的垂线交y轴于点D，且OD=CD=CE．点C的坐标为（a，b），a、b（a＞b）是方程x2-12x+32=0的解．
如图所示，直线y=k1x+b与反比例函数y=
如图，直线l1的函数解析式为y=2x-2，直线l1与x轴交于点D．直线l2：y=kx+b与x轴交于点A，且经过点B，如图所示．直线l1、l2交于点C（m，2）．