Question

如图，在一个房间内，有一个梯子斜靠在墙上，梯子顶端距地面的垂直距离MA为a米，此时梯子的倾斜角为75°，如果梯子的底端不动，顶端靠在对面墙上，此时梯子的顶端距地面的垂直距离NB为b米，梯子的倾斜角为45°，则这间房子的宽AB为（　　）

• A、

  a+b

  2

  米
• B、

  a-b

  2

  米
• C、b米
• D、a米

Answer 1

分析：根据CM=CN以及∠MCN的度数可得到△CMN为等边三角形．利用相应的三角函数表示出MN，MC的长，可得到房间宽AB和AM长相等．

解答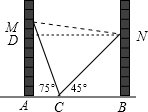：解：过N点作MA垂线，垂足点D，连接NM．
设梯子底端为C点，AB=x，且AB=ND=x．
∴△BNC为等腰直角三角形，
∴180°-45°-75°=60°
∴△CNM为等边三角形，梯子长度相同
∵∠NCB=45°，
∴∠DNC=45°，
∴∠MND=60°-45°=15°，
∴cos15°=

x

MN

，
又∵∠MCA=75°，
∴∠AMC=15°，
∴cos15°=

MA

MC

，
故可得：

x

MN

=

MA

CM

．
∵△CNM为等边三角形，
∴NM=CM．
∴x=MA=a．
故选D．

点评：此题是解直角三角形的知识解决实际生活中的问题，作辅助线很关键．