题目内容
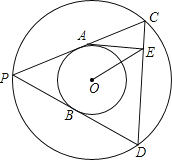
【题目】如图,以O为圆心的两个同心圆,大圆半径为5,小圆半径为![]() ,点P为大圆上的一点,PC、PB切小圆于点A、点B,交大圆于C、D两点,点E为弦CD上任一点,则AE+OE的最小值为 .
,点P为大圆上的一点,PC、PB切小圆于点A、点B,交大圆于C、D两点,点E为弦CD上任一点,则AE+OE的最小值为 .
【答案】![]() .
.
【解析】
试题分析:连接PO,并延长OP到O′交CD于点G,使OG=O′G,连接AO′交CD于点E,连接OE,过点A作AF⊥OP,垂足为F,由切线的性质可知OB⊥PD,由垂径定理可知PB=BD,在Rt△OPB中,由勾股定理可知PB=2![]() ,故此PD=4
,故此PD=4![]() ,同理可知PC=4
,同理可知PC=4![]() ,从而得到PC=PD,然后证明PO平分∠CPD,由等腰三角形三线合一的性质可知PG⊥DC,依据锐角三角函数的定义可知OF=1,AF=2,PG=8,从而求得OO′=7,在Rt△AFO′中,由勾股定理可知AO′=
,从而得到PC=PD,然后证明PO平分∠CPD,由等腰三角形三线合一的性质可知PG⊥DC,依据锐角三角函数的定义可知OF=1,AF=2,PG=8,从而求得OO′=7,在Rt△AFO′中,由勾股定理可知AO′=![]() .
.
解:如图所示:连接PO,并延长OP到O′交CD于点G,使OG=O′G,连接AO′交CD于点E,连接OE,过点A作AF⊥OP,垂足为F.
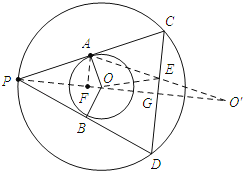
∵PB是小圆的切线,
∴OB⊥PD.
∴PB=BD.
在Rt△OPB中,PB=![]() =
=![]() =2
=2![]() .
.
∴PD=4![]() .
.
同理:PC=4![]() .
.
∴PC=PD.
∵PA、PB是小圆的切线,
∴PO平分∠CPD.
∴PG⊥DC.
∴CD是OO′的垂直平分线.
∴OE=O′E.
∴AE+EO=AE+EO′=AO′.
∵cos∠AOF=![]() =
=![]() ,
,
∴OF=AO×cos∠AOF=![]() =1,AF=2OF=2.
=1,AF=2OF=2.
∵PG=PC×![]() =
=![]() =8,
=8,
∴OG=PG﹣OP=3.
∴OO′=1+3+3=7.
在Rt△AFO′中,AO′=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目



