题目内容
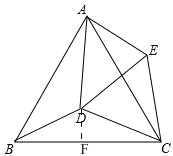
【题目】如图,已知等边△ABC,点D为△ABC内一点,连接DA、DB、DC,∠ADB=120°.以CD为边向CD上方作等边△CDE,连接AE.(0°<∠ACE<60°)
(1)求证:△BDC≌△AEC;
(2)若DA=![]() +1,DB=
+1,DB=![]() ﹣1,DC=2n(n为大于1的整数),求∠BDC的度数;
﹣1,DC=2n(n为大于1的整数),求∠BDC的度数;
(3)若△ADE为等腰三角形,求![]() 的值.
的值.
【答案】(1)证明详见解析;(2)150°;(3)![]() .
.
【解析】
试题分析:(1)由等边三角形的性质得出结论,直接用SAS得出结论;
(2)用等边三角形的性质得出DE=CD,进而判断出△ADE是直角三角形,即可得出结论;
(3)分三种情况先判断出△ADE是等边三角形,进而构造出直角三角形,用含30°的直角三角形的性质得出结论即可.
试题解析:(1)∵△ABC和△CDE是等边三角形,
∴BC=AC,CD=CE=DE,∠ACB=∠DCE=∠CED=60°,
∴∠BCD=∠ACE,
在△BDC和△AEC中,
BC=AC,∠BCD=∠ACE,CE=CE,
∴△BDC≌△AEC(SAS);
(2)由(1)知,DE=CD=2n,△BDC≌△AEC,
∴∠BDC=∠AEC,AE=BD=![]() ﹣1,
﹣1,
∵DA=![]() +1,AE=
+1,AE=![]() ﹣1,DE=2n,
﹣1,DE=2n,
∴![]() =
=![]() =
=![]() ,
,
∴△ADE是直角三角形,
∴∠AED=90°,
∴∠BDC=∠AEC=∠AED+∠CED=150°;
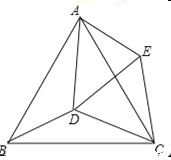
(3)如图,
①当AD=AE时,由(1)知,△BDC≌△AEC,
∴∠CAE=∠CBD,AE=BD,
∴AD=BD,
∵∠ADB=120°,
∴∠BAD=∠ABD=30°,
∵∠ABC=∠BAC=60°,
∴∠CBD=∠CAD=∠CAE=30°,
∴∠DAE=60°,
∴△ADE是等边三角形;
②当AD=DE时,∵CD=DE,
∴AD=CD,
∴∠CAD=∠DCA,
∵∠BAC=∠BCA,
∴∠BAD=∠BCD,
在△ABD和△CBD中,
AB=BC,∠BAD=∠BCD,AD=CD,
∴△ABD≌△CBD,
∴∠ABD=![]() ∠ABC=30°,
∠ABC=30°,
以后同①的方法得出,△ADE是等边三角形,
③当AE=DE时,同②的方法得出,△ADE是等边三角形,
即:△ADE是等边三角形
过点D作DF⊥BC,
∴BC=2CF,在Rt△CDF中,∠DCF=30°,
∴cos30°=![]() ,
,
∴![]() =
=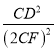 =
=![]() .
.