题目内容
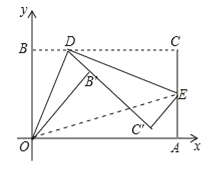
【题目】如图，将矩形纸片ABCD置于直角坐标系中，点A（4，0），点B（0，3），点D（异于点B、C）为边BC上动点，过点O、D折叠纸片，得点B′和折痕OD．过点D再次折叠纸片，使点C落在直线DB′上，得点C′和折痕DE，连接OE，设BD=t．
（1）当t=1时，求点E的坐标；
（2）设S四边形OECB=s，用含t的式子表示s（要求写出t的取值范围）；
（3）当OE取最小值时，求点E的坐标．
【答案】（1）（4，2）；（2）S=
（0＜t＜4）；（3）（4，
）．
【解析】
试题分析：（1）根据折叠的性质和全等三角形的判定定理证明△BOD≌△CDE，求出CE，计算出AE，得到点E的坐标；
（2）根据相似三角形的性质用t表示出CE，根据梯形的面积公式用t表示S；
（3）根据二次函数的性质求出AE的最小值，求出点E的坐标．
试题解析：（1）由折叠的性质可知，∠ODB=∠ODB′，∠EDC=∠EDC′，∴∠ODE=90°，∴∠BDO+∠CDE=90°，又∠BDO+∠BOD=90°，∴∠BOD=∠CDE，∵BD=t=1，BC=4，∴CD=3，又OB=3，∴OB=CD，在△BOD和△CDE中，∵∠B=∠C，OB=CD，∠BOD=∠CDE，∴△BOD≌△CDE，∴CE=BD=1，∴AE=AC﹣CE=2，∴点E的坐标为（4，2）；
（2）∵BD=t，∴DC=BC﹣BD=4﹣t，由（1）得，∠BOD=∠CDE，又∠B=∠C=90°，∴△ODB∽△DCE，∴
，即
，解得，CE=
，∴S=
×（CE+OB）×BC=×（+3）×4，∴S=（0＜t＜4）；
（3）在Rt△OEA中，OE2=OA2+AE2=42+AE2，∴当AE最小时，OE最小，由（2）得，CE=，∴AE=AC﹣CE=
=
，当t=2时，AE的最小值为，此时点E的坐标为（4，）．
