题目内容
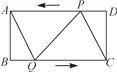
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
【答案】(1)t=4;(2)t=3;(3)周长为20cm,面积为20cm2
【解析】试题分析:(1)当四边形ABQP是矩形时,BQ=AP,据此求得t的值;
(2)当四边形AQCP是菱形时,AQ=AC,列方程求得运动的时间t;
(3)菱形的四条边相等,则菱形的周长=4t,面积=矩形的面积-2个直角三角形的面积.
试题解析:(1)当四边形ABQP是矩形时,BQ=AP,即:t=8-t,
解得t=4.
答:当t=4时,四边形ABQP是矩形;
(2)设t秒后,四边形AQCP是菱形
当AQ=CQ,即![]() =8-t时,四边形AQCP为菱形.
=8-t时,四边形AQCP为菱形.
解得:t=3.
答:当t=3时,四边形AQCP是菱形;
(3)当t=3时,CQ=5,则周长为:4CQ=20cm,
面积为:4×8-2×![]() ×3×4=20(cm2).
×3×4=20(cm2).

练习册系列答案
相关题目