题目内容
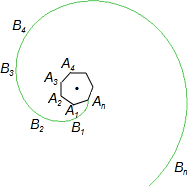 如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为________.
如图,正多边形A1、A2、A3、A4…An,曲线B1B2B3B4…Bn叫做“正多边形的渐开线”,其中AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环.循环一周就叫一周曲线长,当A1A2=1时,一周曲线长为________.
(n+1)π
分析:观察图中可以发现曲线EFGHIJ的长度是由n个从小到大的扇形弧长组成的,所以利用弧长公式即可求出.
解答: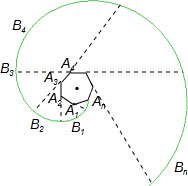 解:正多边形A1A2A3A4…An,的每个外角都等于
解:正多边形A1A2A3A4…An,的每个外角都等于 ,
,
∵AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环,当A1A2=1时,
∴半径依次为1、2、3、…,n,
∴一周曲线长=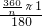 +
+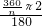 +
+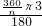 +…+
+…+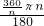 =
= (1+2+3+…+n)π=
(1+2+3+…+n)π= •
• π=(n+1)π.
π=(n+1)π.
故答案为(n+1)π.
点评:本题考查了弧长的计算:弧长= (n为弧所对的圆心角的度数,R为圆的半径).也考查了正多边形的性质.
(n为弧所对的圆心角的度数,R为圆的半径).也考查了正多边形的性质.
分析:观察图中可以发现曲线EFGHIJ的长度是由n个从小到大的扇形弧长组成的,所以利用弧长公式即可求出.
解答:
 解:正多边形A1A2A3A4…An,的每个外角都等于
解:正多边形A1A2A3A4…An,的每个外角都等于 ,
,∵AnB1、B1B2、B2B3、B3B4…的圆心依次按A1、A2、A3、A4…循环,当A1A2=1时,
∴半径依次为1、2、3、…,n,
∴一周曲线长=
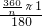 +
+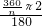 +
+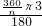 +…+
+…+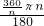 =
= (1+2+3+…+n)π=
(1+2+3+…+n)π= •
• π=(n+1)π.
π=(n+1)π.故答案为(n+1)π.
点评:本题考查了弧长的计算:弧长=
 (n为弧所对的圆心角的度数,R为圆的半径).也考查了正多边形的性质.
(n为弧所对的圆心角的度数,R为圆的半径).也考查了正多边形的性质. 
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 27、我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1是由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,由复制形成的多边形中的任意两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.
27、我们约定,若一个三角形(记为△A1)是由另一个三角形(记为△A)通过一次平移,或绕其任一边的中点旋转180°得到的,则称△A1是由△A复制的.以下的操作中每一个三角形只可以复制一次,复制过程可以一直进行下去.如图1是由△A复制出△A1,又由△A1复制出△A2,再由△A2复制出△A3,形成了一个大三角形,记作△B.以下各题中的复制均是由△A开始的,由复制形成的多边形中的任意两个小三角形(指与△A全等的三角形)之间既无缝隙也无重叠.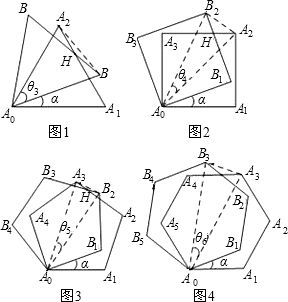
 26、阅读:
26、阅读: