题目内容
【题目】如图，点M，N在半圆的直径AB上，点P，Q在 
上，四边形MNPQ为正方形．若半圆的半径为 
，则正方形的边长为 ． 
【答案】2
【解析】解：连接OP，设正方形的边长为a，则ON= 
，PN=a，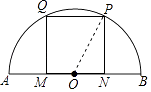 
在Rt△OPN中，
ON2+PN2=OP2，即（ ）2+a2=（ 
）2，解得a=2．
所以答案是：2．
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
