题目内容
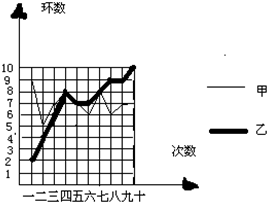 甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
(1)请填写下表:
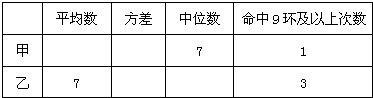
| 平均数 | 方差 | 中位数 | 命中9环以上次数 | |
| 甲 | 7 | 1.2 | 1 | |
| 乙 | 5.4 |
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和中位数相结合看(分析谁的成绩更好些);
③从平均数和命中9环及以上的次数相结合看(分析谁的成绩更好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
解:(1)
(2)测试结果分析
①从平均数和方差来结合看,两者平均数相等,但甲的方差(1.2)小于乙的方差(5.4),所以甲的成绩更稳定;
②从平均数和中位数相结合看,两者平均数相等,但甲的中位数(7)小于乙的中位数(7.5),所以乙的成绩更好些;
③从平均数和命中9环及以上的次数相结合看,两者平均数相等,但甲命中9环及以上的次数(1次)小于乙命中9环及以上的次数(3次),所以乙的成绩更好些;
④从折线图上两人射击命中环数的走势看,乙命中环数的曲线整体呈上升趋势,所以乙更有潜力.
分析:(1)甲的10次射击成绩为:5,6,6,7,7,7,7,8,8,9;中位数是7,命中9环及以上的次数为1次;
乙的10次射击成绩为:2,4,6,7,7,8,8,9,9,10;乙的平均数=(2+4+6+7+7+8+8+9+9+10)÷10=7;命中9环及以上的次数为3次;
(2)①根据平均数和方差的意义分析;②根据平均数和中位数的概念分析;③从平均数和命中9环及以上的次数相结合分析;④从折线图上两人射击命中环数的走势分析.
点评:平均数、众数及中位数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同.
平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动.众数着眼于对各数据出现的频数的考查,其大小只与这组数据中的部分数据有关.
当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量,中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响.当一组数据中的个别数据变动较大时,可用它来描述其集中趋势.

(2)测试结果分析
①从平均数和方差来结合看,两者平均数相等,但甲的方差(1.2)小于乙的方差(5.4),所以甲的成绩更稳定;
②从平均数和中位数相结合看,两者平均数相等,但甲的中位数(7)小于乙的中位数(7.5),所以乙的成绩更好些;
③从平均数和命中9环及以上的次数相结合看,两者平均数相等,但甲命中9环及以上的次数(1次)小于乙命中9环及以上的次数(3次),所以乙的成绩更好些;
④从折线图上两人射击命中环数的走势看,乙命中环数的曲线整体呈上升趋势,所以乙更有潜力.
分析:(1)甲的10次射击成绩为:5,6,6,7,7,7,7,8,8,9;中位数是7,命中9环及以上的次数为1次;
乙的10次射击成绩为:2,4,6,7,7,8,8,9,9,10;乙的平均数=(2+4+6+7+7+8+8+9+9+10)÷10=7;命中9环及以上的次数为3次;
(2)①根据平均数和方差的意义分析;②根据平均数和中位数的概念分析;③从平均数和命中9环及以上的次数相结合分析;④从折线图上两人射击命中环数的走势分析.
点评:平均数、众数及中位数都是描述一组数据的集中趋势的特征数,但描述的角度和适用范围有所不同.
平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动.众数着眼于对各数据出现的频数的考查,其大小只与这组数据中的部分数据有关.
当一组数据中有不少数据多次重复出现时,其众数往往是我们关心的一种统计量,中位数则仅与数据的排列位置有关,某些数据的变动对它的中位数没有影响.当一组数据中的个别数据变动较大时,可用它来描述其集中趋势.

练习册系列答案
相关题目
甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
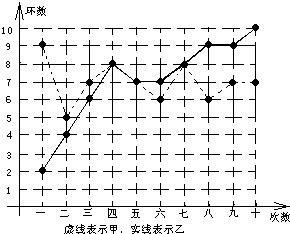
(1)请填写下表:
(2)请你就下列两个不同的角度对这次测试结果进行分析.
①从平均数和方差相结合看,分析谁的成绩好些;
②从平均数和命中9环以上的次数相结合看,分析谁的成绩好些.

(1)请填写下表:
| 平均数 | 方差 | 中位数 | 命中9环以上次数 | |
| 甲 | 7 | 1.2 | 1 | |
| 乙 | 5.4 |
①从平均数和方差相结合看,分析谁的成绩好些;
②从平均数和命中9环以上的次数相结合看,分析谁的成绩好些.

 24、甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如左图所示(实线是甲,虚线是乙)
24、甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如左图所示(实线是甲,虚线是乙) 20、甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如表格:
20、甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如表格:
 甲、乙两人在相同条件下各射靶10次,每次射靶成绩情况如图所示.
甲、乙两人在相同条件下各射靶10次,每次射靶成绩情况如图所示.