题目内容
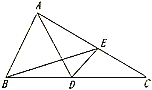
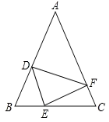
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 边上,且
边上,且![]() ,
,![]() .
.
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)当![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)见解析;(2)68°
【解析】
(1)根据条件即可证明△BDE≌△CEF,由全等三角形的性质得到DE=EF,即可得![]() 是等腰三角形;
是等腰三角形;
(2)先求出∠B的值,由(1)知∠BDE=∠CEF,由外角定理可得∠DEF=∠B.
(1)证明:∵![]() ,
,
∴∠B=∠C,
在△BDE和△CEF中,
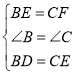 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,则![]() 是等腰三角形;
是等腰三角形;
(2)解:∵![]() ,
,![]() ,
,
∴∠B=∠C=![]() ,
,
由(1)知△BDE≌△CEF,
∴∠BDE=∠CEF,
∵∠DEC=∠BDE+∠B,
∴∠CEF+∠DEF=∠BDE+∠B,即∠BDE+∠DEF=∠BDE+∠B,
∴∠DEF=∠B=68°.

练习册系列答案
相关题目