题目内容
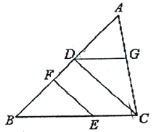
【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.
(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.

【答案】证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,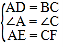 ,
,
∴△ADE≌△CBF(SAS)。
(2)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵AE=CF,∴DF=EB。∴四边形DEBF是平行四边形。
又∵DF=FB,∴四边形DEBF为菱形。
【解析】
试题(1)首先根据平行四边形的性质可得AD=BC,∠A=∠C,再加上条件AE=CF可利用SAS证明△ADE≌△CBF;
(2)首先证明DF=BE,再加上条件AB∥CD可得四边形DEBF是平行四边形,又DF=FB,可根据邻边相等的平行四边形为菱形证出结论.
试题解析:(1)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
∵在△ADE和△CBF中,
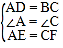 ,
,
∴△ADE≌△CBF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴DF=EB,
∴四边形DEBF是平行四边形,
又∵DF=FB,
∴四边形DEBF为菱形.

【题目】购买甲、乙、丙三种不同品种的练习本各四次,其中,有一次购买时,三种练习本同时打折,四次购买的数量和费用如下表:
购买次数 | 购买各种练习本的数量(单位:本) | 购买总费用(单位:元) | ||
甲 | 乙 | 丙 | ||
第一次 | 2 | 3 | 0 | 24 |
第二次 | 4 | 9 | 6 | 75 |
第三次 | 10 | 3 | 0 | 72 |
第四次 | 10 | 10 | 4 | 88 |
(1)第______次购物时打折;练习本甲的标价是_____元/本,练习本乙的标价是______元/本,练习本丙的标价是______元/本;
(2)如果三种练习本的折扣相同,请问折扣是打几折?
(3)现有资金100.5元,全部用于购买练习本,计划以标价购进练习本36本,如果购买其中两种练习本,请你直接写出一种购买方案,不需说明理由.