题目内容
【题目】已知:如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是( )
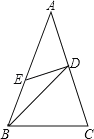
A.30°B.36°C.45°D.50°
【答案】C
【解析】
根据AB=AC,BC=BD,AD=DE=EB可得到几组相等的角,再根据三角形外角的性质可得到∠C,∠A,∠EBD之间的关系,再根据三角形内角和定理即可求解.
解:设∠EBD=x°,
∵BE=DE,
∴∠EDB=∠EBD=x°,
∴∠AED=∠EBD+∠EDB=2x°,
∵AD=DE,
∴∠A=∠AED=2x°,
∴∠BDC=∠A+∠ABD=3x°,
∵BD=BC,
∴∠C=∠BDC=3x°,
∵AB=AC,
∴∠ABC=∠C=3x°,
∵∠A+∠ABC+∠C=180°,
∴2x+3x+3x=180,
解得:x=22.5,
∴∠A=2x°=45°.
故选:C.

练习册系列答案
相关题目
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
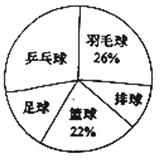
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.