题目内容
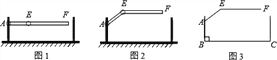
【题目】如图,已知![]() 和
和![]() 都是
都是![]() 的余角,
的余角,![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的角平分线,如果
的角平分线,如果![]()
(1)求![]() 的度数;
的度数;
(2)求![]() 的度数.
的度数.
【答案】(1)50°;(2)90°
【解析】
(1)根据∠AOB和∠COD都是∠BOC的余角,则∠AOB=∠COD=90°∠BOC,再有∠AOD=∠AOB+∠BOD=∠AOB+90°,及∠AOD=130°,可得∠BOC的度数;
(2)由(1)可知∠BOC =50°,结合角平分线定义,可得∠EOB、∠COF度数,再加∠BOC的度数即可.
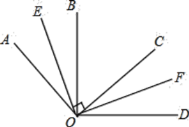
解:(1)∵∠AOB和∠COD都是∠BOC的余角,
∴∠AOB=90°∠BOC ,
∵∠AOD=∠AOB+∠BOD=∠AOB+90°
又∵∠AOD=130°,
∴90°∠BOC+90°=130°,
∴∠BOC =50°;
(2)∵∠AOB和∠COD都是∠BOC的余角,
∴∠AOB=∠COD=40°,
∵OE、OF分别为∠AOB和∠COD的角平分线
∴∠AOE=∠BOE=∠COF=∠DOF=![]() ×40°=20°,
×40°=20°,
∴∠EOF=∠BOE+∠BOC+∠COF=20°+50°+20°=90°.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案【题目】为了促进全民健身运动的开展,某市组织了一次足球比赛,下表记录了比赛过程中部分代表队的积分情况.
代表队 | 场次(场) | 胜(场) | 平(场) | 负(场) | 积分(分) |
| 6 | 5 | 1 | 0 | 16 |
| 6 | 6 | 0 | 0 | 18 |
| 6 | 3 | 2 | 1 | 11 |
| 6 | 3 | 1 | 2 | 10 |
(1)本次比赛中,胜一场积______分;
(2)参加此次比赛的![]() 代表队完成10场比赛后,只输了一场,积分是23分,请你求出
代表队完成10场比赛后,只输了一场,积分是23分,请你求出![]() 代表队胜出的场数.
代表队胜出的场数.
【题目】“姹紫嫣红苗木种植基地”尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元/株的果苗,售后经过统计得到此果苗,单价在第x天(x为整数)销售的相关信息,如下图表所示:
销售量n(株) |
|
销售单价 m(元/株) | 当1≤x≤20时,m=________ |
当21≤x≤30时, |
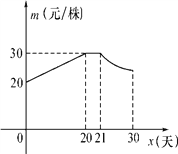
(1)①请将表中当1≤x≤20时,m与x间关系式补充完整;
②计算第几天该果苗单价为25元/株?
(2)求该基地销售这种果苗30天里每天所获利润y(元)关于x(天)的函数关系式;
(3)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”。试问:基地负责人这次为“精准扶贫”捐赠多少钱?