题目内容
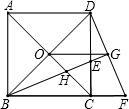 如图,在正方形ABCD中,对角线AC、BD交于点O,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,AC交BG于点H,连接OG,下列结论:①OG∥AD;②△CHE为等腰三角形;③BH=GH;④tan∠F=2;⑤S△BCE:S△BDE=1:
如图,在正方形ABCD中,对角线AC、BD交于点O,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,AC交BG于点H,连接OG,下列结论:①OG∥AD;②△CHE为等腰三角形;③BH=GH;④tan∠F=2;⑤S△BCE:S△BDE=1:| 2 |
| A、①②⑤ | B、①②③ |
| C、②③④ | D、②④⑤ |
分析:正方形的四个边相等,四个角都是直角,根据这可以证明三角形全等,进而证明相似,得到解,也可以用正方形的性质,求角的度数边的长,进而求出三角函数和面积从而得到解.
解答:解:∵△BCE≌△DCF,
∴∠CBE=∠CDF,
∵∠BEC=∠DEG,
∴∠DGB=∠BCE=90°,
∴BG垂直且平分DF,
∵O是BD的中点,
∴OG∥BF,
∴OG∥AD.
所以①选项正确.
∵正方形ABCD,
∴∠DBC=45°,∠BOC=90°,∠BCD=90°,
∵BE平分∠DBC,
∴∠OBH=∠CBH=22.5°,
∴∠EHC=∠OHB=180°-90°-22.5°=67.5°,
∠BEC=180°-90°-22.5°=67.5°=∠EHC,
∴CH=CE,∴②正确;
∵OB≠BC,
∴OH≠CH,
∵OG∥BC,
∴BH≠GH,∴③错误;
∵tan∠F=
,CD≠2CF,
∴tan∠F≠2,∴④错误;
∵∠DBH=∠HBC,
∵四边形ABCD是正方形,BD是对角线,
∴
=cos45°=
,
∴
=
=
,
∵△BDE和△BCE的高都是BC,
∴S△BCE:S△BDE=(
BC×CE):(
BC×DE)=1:
,∴⑤正确;
故选A.

∴∠CBE=∠CDF,
∵∠BEC=∠DEG,
∴∠DGB=∠BCE=90°,
∴BG垂直且平分DF,
∵O是BD的中点,
∴OG∥BF,
∴OG∥AD.
所以①选项正确.
∵正方形ABCD,
∴∠DBC=45°,∠BOC=90°,∠BCD=90°,
∵BE平分∠DBC,
∴∠OBH=∠CBH=22.5°,
∴∠EHC=∠OHB=180°-90°-22.5°=67.5°,
∠BEC=180°-90°-22.5°=67.5°=∠EHC,
∴CH=CE,∴②正确;
∵OB≠BC,
∴OH≠CH,
∵OG∥BC,
∴BH≠GH,∴③错误;
∵tan∠F=
| CD |
| CF |
∴tan∠F≠2,∴④错误;
∵∠DBH=∠HBC,
∵四边形ABCD是正方形,BD是对角线,
∴
| BC |
| BD |
| ||
| 2 |
∴
| BD |
| BC |
| DE |
| CE |
| ||
| 1 |
∵△BDE和△BCE的高都是BC,
∴S△BCE:S△BDE=(
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
故选A.
点评:本题考查了正方形的性质,全等三角形的判定和性质,以及三角函数的定义,三角形的面积等,但本题是个选择题,考试时可用排除法很快得到答案.

练习册系列答案
相关题目
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6