题目内容
已知直线l与⊙O交于不同的两点E,F,CD是⊙O的直径,CA⊥l,DB⊥l,垂足分别为A,B.若AB=7,BD-AC=1,AE=1,试问在线段AB上是否存在点P,使得以点P,A,C为顶点的三角形与以点P,B,D为顶点的三角形相似?若存在,求出AP的长;若不存在,请说明理由.
(1)若l与直径CD不相交,如图所示,
(i)作OH⊥AB于H,易得AE=BF,此时△ACE∽△BED,△AFC∽△BDF,
则E,F为满足的点,故AP=AE=1或AP=AF=AB-BF=6
(ii)若除E,F外还存在点P使△APC∽△BPD,设AC=x,BD=y,则y-x=1,
∵Rt△ACE∽Rt△BED,故
=
,得xy=6
于是x=2,y=3或x=-3,y=-2(舍去)
∵△APC∽△BPD,故
=
,即
=
,解得AP=
,
故存在第三个满足条件的点P,且AP=
.
综合(i),(ii),满足条件的点有三个,AP的长分别为1,6,
.
(2)若l与直径CD相交,且交点为Q,如图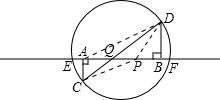
(i)由∠AQC=∠DQB,得Rt△ACQ∽Rt△BDQ,则点Q为满足条件的点,
设AC=x,BD=y,则y-x=1,
又∠DEB=∠ECA,则Rt△ACE∽Rt△BED,
故
=
,得xy=8,
于是,x=
,y=
或x=
,y=
(舍去)
∵Rt△ACQ∽Rt△BDQ,∴
=
,解得AQ=
.
(ii)若除Q外,还存在点P,使△APC∽△BDP,则
=
,
整理得AP2-7AP+8=0,解得AP=
.
综合(i),(ii),满足条件的点P有三个,AP的长分别为
,
,
.
所以,综合(1)(2)可得,满足条件的点共有6个.AP的长度为:
1,6,
,
,
,
.
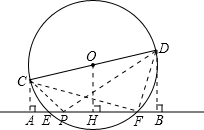
(i)作OH⊥AB于H,易得AE=BF,此时△ACE∽△BED,△AFC∽△BDF,
则E,F为满足的点,故AP=AE=1或AP=AF=AB-BF=6
(ii)若除E,F外还存在点P使△APC∽△BPD,设AC=x,BD=y,则y-x=1,
∵Rt△ACE∽Rt△BED,故
| x |
| AE |
| EB |
| y |
于是x=2,y=3或x=-3,y=-2(舍去)
∵△APC∽△BPD,故
| AP |
| AC |
| BP |
| BD |
| AP |
| 2 |
| 7-AP |
| 3 |
| 14 |
| 5 |
故存在第三个满足条件的点P,且AP=
| 14 |
| 5 |
综合(i),(ii),满足条件的点有三个,AP的长分别为1,6,
| 14 |
| 5 |
(2)若l与直径CD相交,且交点为Q,如图

(i)由∠AQC=∠DQB,得Rt△ACQ∽Rt△BDQ,则点Q为满足条件的点,
设AC=x,BD=y,则y-x=1,
又∠DEB=∠ECA,则Rt△ACE∽Rt△BED,
故
| AC |
| BE |
| AE |
| BD |
于是,x=
| ||
| 2 |
| ||
| 2 |
-
| ||
| 2 |
-
| ||
| 2 |
∵Rt△ACQ∽Rt△BDQ,∴
| AQ |
| QB |
| AC |
| BD |
231-7
| ||
| 66 |
(ii)若除Q外,还存在点P,使△APC∽△BDP,则
| AP |
| BD |
| AC |
| PB |
整理得AP2-7AP+8=0,解得AP=
7±
| ||
| 2 |
综合(i),(ii),满足条件的点P有三个,AP的长分别为
231-7
| ||
| 66 |
7+
| ||
| 2 |
7-
| ||
| 2 |
所以,综合(1)(2)可得,满足条件的点共有6个.AP的长度为:
1,6,
| 14 |
| 5 |
231-7
| ||
| 66 |
7+
| ||
| 2 |
7-
| ||
| 2 |


练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
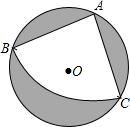



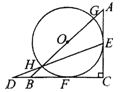
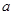 ,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .
,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .