Question

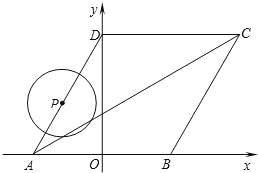
【题目】如图所示，菱形ABCD的顶点A、B在x轴上，点A在点B的左侧，点D在y轴的正半轴上，∠BAD=60°，点A的坐标为（﹣2，0）．

（1）求C点的坐标；

（2）求直线AC的函数关系式；

（3）动点P从点A出发，以每秒1个单位长度的速度，按照A→D→C→B→A的顺序在菱形的边上匀速运动一周，设运动时间为t秒．求t为何值时，以点P为圆心、以1为半径的圆与对角线AC相切？

Answer 1

【答案】（1）C（4，2）；

（2）直线AC的解析式为：y=x+；

（3）当t=2、6、10、14时，以点P为圆心、以1为半径的圆与对角线AC相切．

【解析】

试题分析：（1）在Rt△AOD中，根据OA的长以及∠BAD的正切值，即可求得OD的长，从而得到D点的坐标，然后由菱形的邻边相等和对边相互平行来求点C的坐标；

（2）根据点A、C的坐标，利用待定系数法可求得直线AD的解析式．

（3）由于点P沿菱形的四边匀速运动一周，那么本题要分作四种情况考虑：

在Rt△OAD中，易求得AD的长，也就得到了菱形的边长，而菱形的对角线平分一组对角，那么∠DAC=∠BAC=∠BCA=∠DCA=30°；

①当点P在线段AD上时，若⊙P与AC相切，由于∠PAC=30°，那么AP=2R（R为⊙P的半径），由此可求得AP的长，即可得到t的值；

②③④的解题思路与①完全相同，只不过在求t值时，方法略有不同．

试题解析：（1）∵点A的坐标为（﹣2，0），∠BAD=60°，∠AOD=90°，

∴OD=OAtan60°=2，AD=4，

∴点D的坐标为（0，2），

又∵AD=CD，CD∥AB，

∴C（4，2）；

（2）设直线AC的函数表达式为y=kx+b（k≠0），

∵A（﹣2，0），C（4，2），

∴，

解得．

故直线AC的解析式为：y=x+；

（3）∵四边形ABCD是菱形，

∴∠DCB=∠BAD=60°，

∴∠1=∠2=∠3=∠4=30°，

AD=DC=CB=BA=4，（5分）

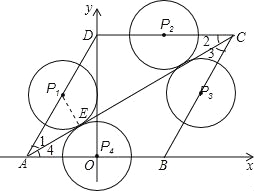
如图所示：

①点P在AD上与AC相切时，

连接P1E，则P1E⊥AC，P1E=r，

∵∠1=30°，

∴AP1=2r=2，

∴t1=2．

②点P在DC上与AC相切时，

CP2=2r=2，

∴AD+DP2=6，

∴t2=6．

③点P在BC上与AC相切时，

CP3=2r=2，

∴AD+DC+CP3=10，

∴t3=10．

④点P在AB上与AC相切时，

AP4=2r=2，

∴AD+DC+CB+BP4=14，

∴t4=14，

∴当t=2、6、10、14时，以点P为圆心、以1为半径的圆与对角线AC相切．