题目内容
【题目】求不等式(2x-1)(x+3)>0的解集.
解:根据“同号两数相乘,积为正”,可得① ![]() 或②
或② ![]() 解①得x>
解①得x> ![]() ;解②得x<-3.
;解②得x<-3.
所以原不等式的解集为x> ![]() 或x<-3.
或x<-3.
请你仿照上述方法解决问题:
(1)求不等式(2x-3)(x+1)<0的解集;
(2)求不等式 ![]() ≥0的解集.
≥0的解集.
【答案】
(1)解: 根据“异号两数相乘,积为负”,可得
① ![]() 或②
或② ![]()
解①,无解;解②,得-1<x< ![]() .
.
所以原不等式的解集为-1<x< ![]() .
.
(2)解:根据“同号两数相除,商为正”及“0除以任何一个不为0的数都得0”,可得① 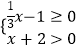 或②
或② 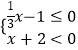
解①得x≥3;解②得x<-2.
所以原不等式的解集为x≥3或x<-2.
【解析】(1)根据“异号两数相乘,积为负”,可得出两个一元一次不等式组,分别解出每一个不等式组的解集,综合两个不等式组的解集,得出原不等式的解集;
(2):根据“同号两数相除,商为正”及“0除以任何一个不为0的数都得0 ,可得出两个一元一次不等式组,分别解出每一个不等式组的解集,综合两个不等式组的解集,得出原不等式的解集。
【考点精析】掌握有理数的乘法法则和有理数的除法是解答本题的根本,需要知道有理数乘法法则:1、两数相乘,同号为正,异号为负,并把绝对值相乘2、任何数同零相乘都得零3、几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定;有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
