��Ŀ����
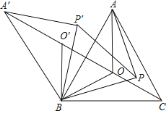
����Ŀ������ͼ��ʾ�������������У�ÿ��С�����εı߳�Ϊ1����������Σ������������ߵĽ���������Σ�ABC�Ķ���A��C������ֱ�Ϊ����4��5��������1��3����
��1������ͼ��ʾ������ƽ��������ƽ��ֱ������ϵ����עԭ���Լ�x�ᡢy�
��2��������ABC����y��ԳƵġ�A��B��C�䣬��д����B������ꣻ
��3����P��x���ϵĶ��㣬��ͼ���ҳ�ʹ��A��BP�ܳ���Сʱ�ĵ�P��ֱ��д����P�������ǣ��� ����

���𰸡���1�������������2��ͼ���������B������꣨2��1������3������1��0����
��������
��1������A��C���������ȷ������ϵ���ɣ�
��2���ֱ�����A��B��C�Ķ�Ӧ��A�䣬B�䣬C�伴�ɣ�
��3������B����x��ĶԳƵ�B�壬����A��B�彻x����p����P��Ϊ����
�⣺��1��ƽ��ֱ������ϵ��ͼ��ʾ��

��2����ͼ��A��B��C�伴Ϊ������ͼ��֪��B�䣨2��1����
��3����ͼ��ʾ����P����1��0����Ϊ����㣮
�ʴ�Ϊ������1��0����

��ϰ��ϵ�д�
 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
�����Ŀ