题目内容
【题目】如图，直线
的解析式为
，且
与
轴交于点D，直线
经过点
、
，直线
、
交于点C．
（1）求直线
的解析表达式；
（2）求
的面积；
（3）在直线
上存在异于点C的另一点P，使得
与
的面积相等，请求出点P的坐标．
【答案】（1）
；（2）
；（3）P（6，3）．
【解析】试题分析：（1）利用待定系数法求直线
的解析表达式；
（2）由方程组
得到C（2，﹣3），再利用x轴上点的坐标特征确定D点坐标，然后根据三角形面积公式求解；
（3）由于△ADP与△ADC的面积相等，根据三角形面积公式得到点D与点C到AD的距离相等，则D点的纵坐标为3，对于函数
，计算出函数值为3所对应的自变量的值即可得到D点坐标．
试题解析：（1）设直线
的解析表达式为
，把A（4，0）、B（3， 
）代入得： 
，解得： 
，所以直线
的解析表达式为
；
（2）解方程组：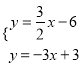 
，得： 
，则C（2，﹣3）；当y=0时， 
，解得x=1，则D（1，0），所以△ADC的面积=
×（4﹣1）×3=
；
（3）因为点D与点C到AD的距离相等，所以D点的纵坐标为3，当y=3时， 
，解得x=6，所以D点坐标为（6，3）．
练习册系列答案
教材全解字词句篇系列答案
相关题目
