题目内容
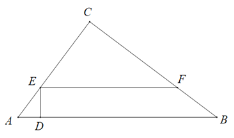
【题目】如图,在直角△ABC中,∠C=90°,AC=15,BC=20,点D为AB边上一动点,若AD的长度为m,且m的范围为0<m<9,在AC与BC边上分别取两点E、F,满足ED⊥AB,FE⊥ED.
(1)求DE的长度;(用含m的代数式表示)
(2)求EF的长度;(用含m的代数式表示)
(3)请根据m的不同取值,探索过D、E、F三点的圆与△ABC三边交点的个数.
【答案】(1)![]() ;(2) 25-
;(2) 25-![]() ; (3)见解析.
; (3)见解析.
【解析】
(1)先证△ADE∽△ACB,得到![]() =
=![]() ,代入即可得到DE=
,代入即可得到DE=![]() ;
;
(2)由勾股定理得到AE=![]() ,利用两个角相等的两个三角形相似得到△ADE∽△ECF,利用相似三角形对应边成比例,得到
,利用两个角相等的两个三角形相似得到△ADE∽△ECF,利用相似三角形对应边成比例,得到![]() =
=![]() ,代入即可得到EF=25-
,代入即可得到EF=25-![]() ;
;
(3)先分别求出过D、E、F三点的⊙O与AC和BC相切时m=![]() 和m=
和m=![]() ,再分0<m<
,再分0<m<![]() ,m=
,m=![]() ,
,![]() <m<
<m<![]() ,m=
,m=![]() ,
,![]() <m<9,五种情况进行说明.
<m<9,五种情况进行说明.
解:(1)∵ED⊥AB,∴∠EDA=90°,∴∠EDA=∠C=90°,
∵∠A=∠A,∴△ADE∽△ACB,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
∴DE=![]() ;
;
(2)在RT△ADE中,
AE=![]() =
=![]() ,
,
∵ED⊥AB,FE⊥ED
∴∠EDA=∠DEF=90°,
∴EF∥AB,
∴∠A=∠CEF,
又∵∠EDA=∠C,
∴△ADE∽△ECF,
∴![]() =
=![]() ,∴m:(15-
,∴m:(15-![]() )=
)=![]() :EF,
:EF,
∴EF=25-![]() .
.
(3)当ED:EF=3:4,⊙O与AC相切于点E,
![]() :(25-
:(25-![]() )=3:4,m=
)=3:4,m=![]() ,
,
当ED:EF=4:3,⊙O与BC相切于点F,
![]() :(25-
:(25-![]() )=4:3,m=
)=4:3,m=![]() ,
,
情况一:当0<m<![]() 时,⊙O与△ABC有六个交点;
时,⊙O与△ABC有六个交点;
情况二:当m=![]() 时,⊙O与△ABC有五个交点;
时,⊙O与△ABC有五个交点;
情况三:当![]() <m<
<m<![]() 时,⊙O与△ABC有六个交点;
时,⊙O与△ABC有六个交点;
情况四:当m=![]() 时,⊙O与△ABC有五个交点;
时,⊙O与△ABC有五个交点;
情况五:当![]() <m<9时,⊙O与△ABC有六个交点.
<m<9时,⊙O与△ABC有六个交点.
故答案为:(1)![]() ;(2) 25-
;(2) 25-![]() ; (3)见解析.
; (3)见解析.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】光明中学全体学生1100人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
(1)填写下表:

中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩(单位:分) |
(2)估计光明中学全体学生社会实践活动成绩的总分.