题目内容
 25、有一块边长为24米的正方形绿地ABCD(如图),在绿地的BC边上距B点7米E处有一健身器,居住在A处的居民经常践踏绿地,沿直线AE直达E处健身,小明同学想在A处树立一块标牌“少走■米,踏之何忍?”则标牌上的“■”处的数字是
25、有一块边长为24米的正方形绿地ABCD(如图),在绿地的BC边上距B点7米E处有一健身器,居住在A处的居民经常践踏绿地,沿直线AE直达E处健身,小明同学想在A处树立一块标牌“少走■米,踏之何忍?”则标牌上的“■”处的数字是6
.分析:在直角△ABE中,AE为斜边,已知AB,BE,则根据勾股定理可以求斜边AE,根据少走的距离为AB+BE-AE可以求解.
解答:解:因为是一块正方形的绿地,所以∠B=90°,由勾股定理得,AE=25米,
计算由A点顺着AB,BE到E点的路程是24+7=31米,而AE=25米,则少走31-25=6米.
故答案为:6.
计算由A点顺着AB,BE到E点的路程是24+7=31米,而AE=25米,则少走31-25=6米.
故答案为:6.
点评:此题主要考查学生对勾股定理在实际生活中的运用能力,同时也增强了学生们要爱护草地的意识.

练习册系列答案
相关题目

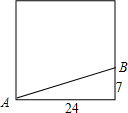 有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走▇米,踏之何忍”请你计算后帮小明在标牌的▇填上适当的数字为:
有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走▇米,踏之何忍”请你计算后帮小明在标牌的▇填上适当的数字为: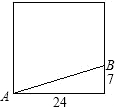 有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走▇米,踏之何忍”,请你计算后帮小明在标牌的▇填上适当的数字.
有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走▇米,踏之何忍”,请你计算后帮小明在标牌的▇填上适当的数字. 知识是用来为人类服务的,我们应该把它们用于有意义地方.就下面的情景请你作出评判.有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍?”请你计算后帮小明在标牌的■处填上适当的数字.
知识是用来为人类服务的,我们应该把它们用于有意义地方.就下面的情景请你作出评判.有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走■米,踏之何忍?”请你计算后帮小明在标牌的■处填上适当的数字.