题目内容
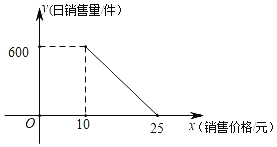
【题目】奏响复工复产“协奏曲”,防疫复产两不误.2020年2月5日,四川省出台《关于应对新型冠状病毒肺炎疫情缓解中小企业生产经营困难的政策措施》,推出减负降成本、破解融资难、财政补贴和税收减免、稳岗支持等13条举措,携手中小企业共渡难关.某企业积极复工复产,生产某种产品成本为9元/件,经过市场调查获悉,日销售量y(件)与销售价格x(元/件)的函数关系如图所示:
(1)求出y与x之间的函数表达式;
(2)当销售价格为多少元时,该企业日销售额为6000元?
(3)若该企业每销售1件产品可以获得2元财政补贴,则当销售价格x为何值时,该企业可以获最大日利润,最大日利润值为多少?
【答案】(1)y=﹣40x+1000;(2)当销售价格为10元或15元时,该企业日销售额为6000元;(3)当销售价格为16元/件时,每天的销售利润最大,最大利润为3240元.
【解析】
(1)设y=kx+b,将点(10,600),(25,0)代入解析式,通过解方程组得到k与b的值;
(2)由题意可知,x(﹣40x+1000)=6000,解出x即可;
(3)设该企业每天获得利润为W元,则W=(﹣40x+1000)(x﹣9+2)=﹣40(x﹣16)2+3240,由此可知当x=16时,W的值最大.
解:(1)设y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴y=﹣40x+1000;
(2)由题意可知,x(﹣40x+1000)=6000,
解得x=10或x=15,
∴当销售价格为10元或15元时,该企业日销售额为6000元;
(3)设该企业每天获得利润为W元,则
W=(﹣40x+1000)(x﹣9+2)=﹣40(x﹣16)2+3240,
∴当销售价格为16元/件时,每天的销售利润最大,最大利润为3240元.

练习册系列答案
相关题目