题目内容
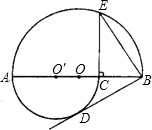
如图,AB是半圆⊙O的直径,AC⊥AB,AB=2AC,BF⊥AB,在直径AB上任取一点P(不与端点A、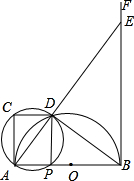 B重合),过A、P、C三点的圆与⊙O相交于除点A以外的另一点D,连接AD并延长交射线BF于点E,连接DB、DP、DC.
B重合),过A、P、C三点的圆与⊙O相交于除点A以外的另一点D,连接AD并延长交射线BF于点E,连接DB、DP、DC.(1)求证:△ACD∽△BPD;
(2)求证:BE=2BP;
(3)试问当点P在何位置时,DE=2AD.
分析:(1)由于四边形APDC是小圆的内接四边形,那么∠BPD=∠C,证两三角形相似需再得出一组对应角相等,由于AC,BE都垂直AB,因此可通过这两条平行线得出∠CAD=∠BED,而∠BED又和∠ABD同为∠DBE的余角,因此可得出∠EBD=∠DAC,这样两组对应角相等可得出两三角形相似.
(2)根据(1)的相似三角形,可以得出关于BP,AC,AD,BD的比例关系式,然后通过相似三角形ADB和ABE可得出关于AD,BD,AB,BE的比例关系式,那么通过置换相等的量,就可得出BE:BP=AB:AC,由此得证.
(3)本题是求BP,AB的比例关系,当DE=2AD时,根据射影定理可得BE2=DE•AE=6AD2,BE=
AD=2BP,BP=
AD,同样根据射影定理可得出AB2=AD•AE=4AD2,AB=2AD,因此BP=
AB,即当BP=
AB时,DE=2AD.
(2)根据(1)的相似三角形,可以得出关于BP,AC,AD,BD的比例关系式,然后通过相似三角形ADB和ABE可得出关于AD,BD,AB,BE的比例关系式,那么通过置换相等的量,就可得出BE:BP=AB:AC,由此得证.
(3)本题是求BP,AB的比例关系,当DE=2AD时,根据射影定理可得BE2=DE•AE=6AD2,BE=
| 6 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:(1)证明:
∵四边形APDC是小圆的内接四边形
∴∠BPD=∠C
∵CA⊥AB,EB⊥AB
∴CA∥BE
∴∠CAD=∠DEB
∵∠DEB+∠DBE=∠DBP+∠DBE=90°
∴∠DBP=∠BEA=∠CAD
∴△ACD∽△BPD.
(2)证明:由(1)知∠BED=∠DBP
∵∠ADB=∠ABE
∴△ADB∽△ABE
∴
=
由(1)的相似三角形可得
=
∴
=
,即
=
=2
∴BE=2BP.
(3)由DB•DB=AD•2DA,得DB:AD=
,
∵△ACD∽△BPD,
∴DB:DA=PB:AC=PB:
=
,
∴PB=
AB时,DE=2AD.
∵四边形APDC是小圆的内接四边形
∴∠BPD=∠C
∵CA⊥AB,EB⊥AB
∴CA∥BE
∴∠CAD=∠DEB
∵∠DEB+∠DBE=∠DBP+∠DBE=90°
∴∠DBP=∠BEA=∠CAD
∴△ACD∽△BPD.
(2)证明:由(1)知∠BED=∠DBP
∵∠ADB=∠ABE
∴△ADB∽△ABE
∴
| AD |
| BD |
| AB |
| BE |
由(1)的相似三角形可得
| AC |
| BP |
| AD |
| BD |
∴
| AB |
| BE |
| AC |
| BP |
| AB |
| AC |
| BE |
| BP |
∴BE=2BP.
(3)由DB•DB=AD•2DA,得DB:AD=
| 2 |
∵△ACD∽△BPD,
∴DB:DA=PB:AC=PB:
| AB |
| 2 |
| 2 |
∴PB=
| ||
| 2 |
点评:本题主要考查了相似三角形的判定和性质,通过相似三角形来得出与已知和所求相关的线段成比例是解题的关键.

练习册系列答案
相关题目
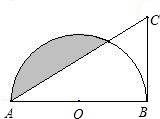 如图,AB是半圆O的直径,∠BAC=30°,BC为半圆的切线,切点为B,且BC=4\sqrt{3}.
如图,AB是半圆O的直径,∠BAC=30°,BC为半圆的切线,切点为B,且BC=4\sqrt{3}.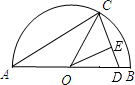 如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE=
如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE=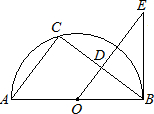 AC交BC于点D,在OD的延长线上取一点E,连接EB,使∠OEB=∠ABC.
AC交BC于点D,在OD的延长线上取一点E,连接EB,使∠OEB=∠ABC.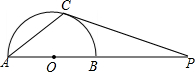 (2013•镇江)如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.若∠CPA=20°,则∠A=
(2013•镇江)如图,AB是半圆O的直径,点P在AB的延长线上,PC切半圆O于点C,连接AC.若∠CPA=20°,则∠A=