题目内容
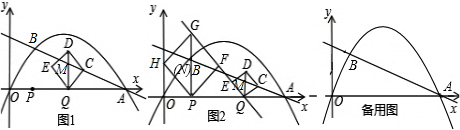
如图1,在平面直角坐标系中,抛物线过原点O,点A(10,0)和点B(2,2),在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P、Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE(正方形QCDE随点Q运动).(1)求这条抛物线的函数表达式;
(2)设正方形QCDE的面积为S,P点坐标(m,0)求S与m之间的函数关系式;
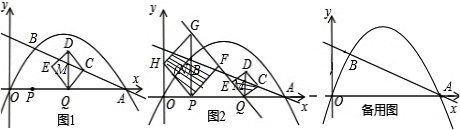
(3)过点P作x轴的垂线,交抛物线于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形PFGH随点P运动),当点P运动到点(2,0)时,如图2,正方形PFGH的边GF和正方形QCDE的边EQ落在同一条直线上.
①则此时两个正方形中在直线AB下方的阴影部分面积的和是多少?
②若点P继续向点A运动,还存在两个正方形分别有边落在同一条直线上的情况,请直接写出每种情况下点P的坐标,不必说明理由.
分析:(1)抛物线与x轴交于O、A两点,设抛物线的交点式,将B点坐标代入,可求抛物线解析式;
(2)根据A(10,0),B(2,2)求直线AB的解析式,由AQ=2OP=2m,得到OQ=OA-AQ=10-2m,代入直线AB的解析式,可求M点纵坐标,得出QD的表达式,根据S=
QD2求解;
(3)①将x=2代入抛物线解析式得y=2,可知N(2,2),G(2,4),当GF和EQ落在同一条直线上时,△FGQ为等腰直角三角形,则PQ=PG=4,OQ=OP+PQ=6,代入直线AB解析式得M(6,1),即QM=1,由旋转法可知,每一个阴影部分面积等所在正方形面积的一半,由此可求两个阴影部分面积和;
②分为PF、DE,PF、CQ,GF、CD三种情况,求出相应的P点坐标.
(2)根据A(10,0),B(2,2)求直线AB的解析式,由AQ=2OP=2m,得到OQ=OA-AQ=10-2m,代入直线AB的解析式,可求M点纵坐标,得出QD的表达式,根据S=
| 1 |
| 2 |
(3)①将x=2代入抛物线解析式得y=2,可知N(2,2),G(2,4),当GF和EQ落在同一条直线上时,△FGQ为等腰直角三角形,则PQ=PG=4,OQ=OP+PQ=6,代入直线AB解析式得M(6,1),即QM=1,由旋转法可知,每一个阴影部分面积等所在正方形面积的一半,由此可求两个阴影部分面积和;
②分为PF、DE,PF、CQ,GF、CD三种情况,求出相应的P点坐标.
解答:解:(1)∵抛物线过O(0,0),A(10,0),
∴设抛物线解析式为y=a(x-0)(x-10),
将B(2,2)代入,得a×2×(2-10)=2,解得a=-
,
∴抛物线解析式为y=-
x(x-10)=-
x2+
x;
(2)设AB解析式为y=kx+n,将A(10,0),B(2,2)代入,
得
,
解得
,
则y=-
x+
,
∵P(m,0),
∴OP=m,AQ=2m,OQ=10-2m,
∴当x=10-2m时,QM=-
(10-2m)+
=
m,
∴QD=m,
∵四边形QCDE是正方形,
∴S=
QD2=
m2;
(3)①由P(2,0),根据抛物线解析式可知N(2,2),
由正方形的性质得G(2,4),即PG=4,
又∵当GF和EQ落在同一条直线上时,△PGQ为等腰直角三角形,
∴PQ=PG=4,OQ=OP+PQ=6,代入直线AB解析式得M(6,1),即QM=1,QD=2,
∴阴影部分面积和=
×(
PG2+
QD2)=5;
②P1(2.5,0),P2(
,0),P3(9-
,0).
∴设抛物线解析式为y=a(x-0)(x-10),
将B(2,2)代入,得a×2×(2-10)=2,解得a=-
| 1 |
| 8 |
∴抛物线解析式为y=-
| 1 |
| 8 |
| 1 |
| 8 |
| 5 |
| 4 |

(2)设AB解析式为y=kx+n,将A(10,0),B(2,2)代入,
得
|
解得
|
则y=-
| 1 |
| 4 |
| 5 |
| 2 |
∵P(m,0),
∴OP=m,AQ=2m,OQ=10-2m,
∴当x=10-2m时,QM=-
| 1 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
∴QD=m,
∵四边形QCDE是正方形,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
(3)①由P(2,0),根据抛物线解析式可知N(2,2),
由正方形的性质得G(2,4),即PG=4,
又∵当GF和EQ落在同一条直线上时,△PGQ为等腰直角三角形,
∴PQ=PG=4,OQ=OP+PQ=6,代入直线AB解析式得M(6,1),即QM=1,QD=2,
∴阴影部分面积和=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②P1(2.5,0),P2(
| 10 |
| 3 |
| 41 |
点评:本题考查了二次函数的综合运用.关键是根据正方形对角线的性质及其与x轴垂直解题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′; 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为

 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 点,这时点
点,这时点 与点
与点 为旋转中心时,点
为旋转中心时,点 点,点
点,点 点,点
点,点 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.


 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐为.
的坐为. ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),