题目内容
【题目】(知识回顾)
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
(理解应用)
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,试求m的值;
(2)若一次函数y=2kx+1﹣4k的图象经过某个定点,则该定点坐标为 ;
(能力提升)
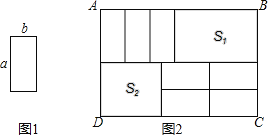
(3)7张如图1的小长方形,长为a,宽为b.按照图2方式不重叠地放在大矩形ABCD内,大矩形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变.求a与b的等量关系.
【答案】(1)m=![]() ;(2)(2,1);(3)a=2b.
;(2)(2,1);(3)a=2b.
【解析】
(1)由题可知代数式的值与x的取值无关,所以含x项的系数为0,故将多项式整理为(2m﹣3)x﹣3m+2m2,令x系数为0,即可求出m.
(2)根据题意可知图象经过某个定点即x取某定值时,函数值与k无关,故可将x作系数,把k看出字母合并同类项,原函数解析式可化为即y=2k(x﹣2)+1,当x﹣2=0时即看求出y值,即定点为(2,1).
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),即可得到S1﹣S2关于x的代数式,根据取值与x可得a=2b.
解:(1)(2x﹣3)m+2m2﹣3x=2mx﹣3m+2m2﹣3x=(2m﹣3)x﹣3m+2m2,
∵若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,
∴2m﹣3=0,
∴m=![]() .
.
(2)∵y=2kx+1﹣4k=2k(x﹣2)+1,
当x=2时,y=1,故一次函数y=2kx+1﹣4k的图象经过定点(2,1),
故答案为:(2,1)
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变.
∴S1﹣S2取值与x无关,
∴a﹣2b=0
∴a=2b.