题目内容
【题目】如图1,矩形ABCD,AB=6cm,AD=8cm,点O从点B出发,以1cm/s的速度向点C运动,设O点运动时间为t(单位:s)(0<t<4),以点O为圆心,OB为半径作半圆⊙O交BC 于点M,过点A作⊙O的切线交BC于点N,切点为P.

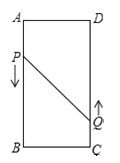
(1)如图2,当点N与点C重合时,求t;
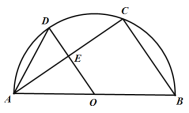
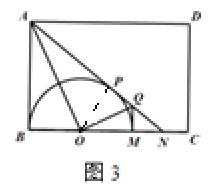
(2)如图3,连接AO,作OQ![]() AO交AN于点Q,连接QM,求证:QM是⊙O的切线;
AO交AN于点Q,连接QM,求证:QM是⊙O的切线;
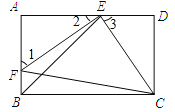
(3)如图4,连接CP,在点O整个运动过程中,求CP的最小值.
【答案】(1)3 ;(2)见解析;(3)4.
【解析】
(1)连接OP,根据切线的性质与矩形的性质得到△ABC∽△OPC,故![]() ,根据勾股定理求出AC,代入即可求出OP,即得到OB的长进行求解.
,根据勾股定理求出AC,代入即可求出OP,即得到OB的长进行求解.
(2)连接OP,证明△OPQ≌△OMQ,得到∠OMQ=∠OPQ=90°,故可证明;
(3)由(2)可知当CP⊥OQ时CP最短,再根据图2利用勾股定理即可求出PC的长.
(1)连接OP,
∵AC是⊙O的切线,∴∠OPC=90°,∵四边形ABCD为矩形,∴∠ABC=90°,
又∠ACB=∠OCP
∴△ABC∽△OPC,
故![]() ,
,
∵AB=6cm,AD=8cm,
∴AC=![]()
又OP=OB
∴![]()
解得OB=3,
∵点O从点B出发,以1cm/s的速度向点C运动,
∴t=3;

(2)连接OP,
∵BO=OP,∴AO平分∠BAC,
∴∠BAO=∠PAO
∵∠ABC=∠APO=90°,
∴∠AOB=∠AOP
∵AO⊥OQ,
∴∠AOQ=90°,
∴∠AOB+∠QOM=90°, ∠AOP+∠QOP=90°,
故∠QOM=∠QOP
又OP=OM,OQ=OQ
∴△OPQ≌△OMQ
∴∠OMQ=∠OPQ=90°,
故QM是⊙O的切线;
(3)由(2)可知当CP⊥OQ时CP最短,
如图2,由(1)可得OC=8-3=5,OP=3,
故CP=![]()
则CP的最小值为4.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案