题目内容
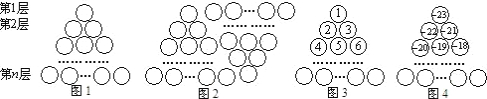
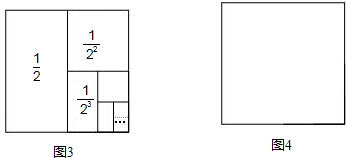
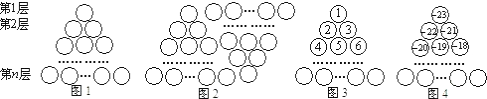
图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=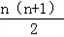
．
．
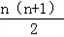如果图1中的圆圈共有12层，
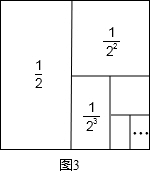
（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是；
（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数﹣23，﹣22，﹣21，…，求图4中所有圆圈中各数的绝对值之和．
（1）我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是；
（2）我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数﹣23，﹣22，﹣21，…，求图4中所有圆圈中各数的绝对值之和．
解：（1）1+2+3+…+11+1=6×11+1=67；
（2）图4中所有圆圈中共有1+2+3+…+12=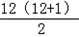
=78个数，
其中23个负数，1个0，54个正数，
所以图4中所有圆圈中各数的绝对值之和为：
|﹣23|+|﹣22|+…+|﹣1|+0+1+2+…+54
=（1+2+3+…+23）+（1+2+3+…+54）
=276+1485
=1761．
（2）图4中所有圆圈中共有1+2+3+…+12=
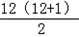=78个数，其中23个负数，1个0，54个正数，
所以图4中所有圆圈中各数的绝对值之和为：
|﹣23|+|﹣22|+…+|﹣1|+0+1+2+…+54
=（1+2+3+…+23）+（1+2+3+…+54）
=276+1485
=1761．
练习册系列答案
相关题目
