题目内容
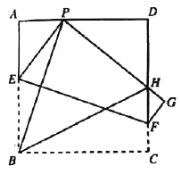
【题目】一张长方形桌子可坐6人，按图3将桌子拼在一起.
（1）2张桌子拼在一起可坐 人，4张桌子拼在一起可坐 人，n张桌子拼在一起可坐 人；
（2）一家餐厅有40张这样的长方形桌子，按照上图的方式每5张拼成1张大桌子，则40张桌子可拼成8张大桌子，共可坐多少人？
【答案】（1）8，12，（4+2n）；（2）共可坐112人.
【解析】
（1）根据题目中的图形，可以发现所座人数的变化规律，从而可以解答本题；
（2）根据（1）中的发现和题意，可以求得40张桌子可拼成8张大桌子，共可坐多少人.
解：（1）由图可得，
2张桌子拼在一起可坐：4+2×2＝4+4＝8（人），
4张桌子拼在一起可坐：4+2×4＝4+8＝12（人），
n张桌子拼在一起可坐：（4+2n）人；
（2）由题意可得，
40张桌子可拼成8张大桌子，共可坐：（4+2×5）×8＝（4+10）×8＝14×8＝112（人），
即40张桌子可拼成8张大桌子，共可坐112人.
【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为（单位：环）：
甲：8，8，7，8，9
乙：5，9，7，10，9
教练根据他们的成绩绘制了如下尚不完整的统计图表：
选手 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 | b | 8 | 0.4 |
乙 | α | 9 | c | 3.2 |
根据以上信息，请解答下面的问题：
（1）α＝ ，b＝ ，c＝ ；
（2）完成图中表示乙成绩变化情况的折线；
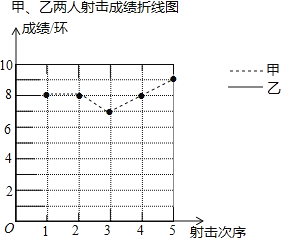
（3）教练根据这5次成绩，决定选择甲参加射击比赛，教练的理由是什么？
（4）若选手乙再射击第6次，命中的成绩是8环，则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 ．（填“变大”、“变小”或“不变”）
【题目】在学校组织的“迎新年，做守法好公民”的知识竞赛中，每班参加比赛的人数相同，成绩分为
四个等级，其中相应等级的得分依次记为100分，90分，80分，70分．学校将某年级的1班和2班的成绩整理并绘制成如下的统计图：
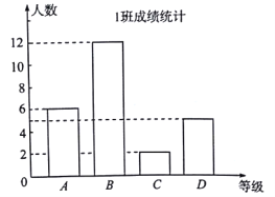
请你根据以上提供的信息解答下列问题：
（1）此次竞赛中，2班成绩在
级以上（包括级）的人数为____人；
（2）请你将表格补充完整：
班级 | 平均数（分） | 中位数（分） | 众数（分） |
1班 | 90 | ||
2班 | 87.6 | 100 |
（3）请从下列不同角度对这次竞赛成绩的结果进行分析；
①从平均数和中位数的角度来比较1班和2班的分成绩；
②从平均数和众数的角度来比较1班和2班的成绩；
③从
级以上（包括级）的人数的角度来比较1班和2班的成绩.
