题目内容
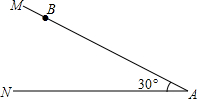 (2013•河南模拟)已知∠MAN=30°,点B是边AM上一点.
(2013•河南模拟)已知∠MAN=30°,点B是边AM上一点.(1)尺规作图(不写作法,保留作图痕迹):
①作线段AB的垂直平分线分别交AB、AN于点C、D;
②在DN上截取DE,使DE=DC,连接BD、BE.
(2)判断BE和AE的位置关系,并给出证明.
分析:(1)利用垂直平分线的作法得出即可,进而得出E的位置;
(2)利用垂直平分线的性质得出BD=AD,进而得出△BED≌△BCD(SAS),则∠BED=∠BCD=90°,即可得出答案.
(2)利用垂直平分线的性质得出BD=AD,进而得出△BED≌△BCD(SAS),则∠BED=∠BCD=90°,即可得出答案.
解答: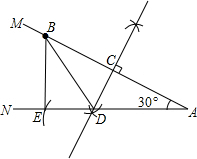 解:(1)如图所示:
解:(1)如图所示:
(2)BE⊥AE,
证明:∵CD是AB的垂直平分线,
∴BD=AD,
∴∠ABD=∠A=30°,
∴∠BDC=∠ADC=60°,
∴∠BDE=180°-60°-60°=60°,
∴∠BDC=∠BDE,
在△BED和△BCD中,
,
∴△BED≌△BCD(SAS),
∴∠BED=∠BCD=90°,
∴BE⊥AE.
 解:(1)如图所示:
解:(1)如图所示:(2)BE⊥AE,
证明:∵CD是AB的垂直平分线,
∴BD=AD,
∴∠ABD=∠A=30°,
∴∠BDC=∠ADC=60°,
∴∠BDE=180°-60°-60°=60°,
∴∠BDC=∠BDE,
在△BED和△BCD中,
|
∴△BED≌△BCD(SAS),
∴∠BED=∠BCD=90°,
∴BE⊥AE.
点评:此题主要考查了线段垂直平分线的作法以及其性质和全等三角形的判定与性质等知识,根据已知得出∠BDC=∠BDE是解题关键.

练习册系列答案
相关题目
 (2013•河南模拟)如图,直线a∥直线b,∠1=∠2,∠3=150°,∠4的大小( )
(2013•河南模拟)如图,直线a∥直线b,∠1=∠2,∠3=150°,∠4的大小( ) (2013•河南模拟)如图,在平面直角坐标系中,Rt△OAB的三个顶点坐标分别是O(0,0),A(-1,2),B(-1,0)将△OAB先向左平移1个单位长度得到△O′A′B′,再将△O′A′B′绕点O′按顺时针方向旋转90°得到△O′A″B″,则点A″的坐标是( )
(2013•河南模拟)如图,在平面直角坐标系中,Rt△OAB的三个顶点坐标分别是O(0,0),A(-1,2),B(-1,0)将△OAB先向左平移1个单位长度得到△O′A′B′,再将△O′A′B′绕点O′按顺时针方向旋转90°得到△O′A″B″,则点A″的坐标是( )