题目内容
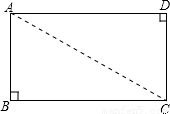
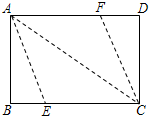
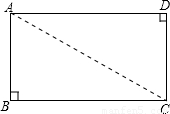
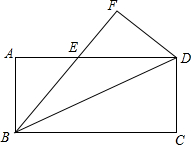 如图,矩形纸片ABCD沿对角线BD折叠,使点C落在点F处,BF交AD于点E.
如图,矩形纸片ABCD沿对角线BD折叠,使点C落在点F处,BF交AD于点E.
(1)若∠CBD=25°,求∠AEB的度数.
(2)求证:△ABE≌△FDE.
解:(1)由折叠可得:∠FBD=∠DBC,
∵∠CBD=25°,
∴∠FBD=25°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEB=∠EBC=25°+25°=50°;
(2)根据折叠可得:DF=AB,∠F=∠C=90°,
∵四边形ABCD是矩形,
∴AB=CD=FD,∠A=∠C=∠F=90°,
∵在△AEB和△FED中,
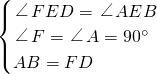 ,
,
∴△ABE≌△FDE(AAS).
分析:(1)根据折叠可得∠FBD=∠DBC,进而可得到∠FBD=25°,再根据两直线平行,内错角相等可得∠AEB的度数;
(2)根据折叠可得:DF=AB,∠F=∠C=90°,根据矩形的性质可得AB=CD=FD,∠A=∠C=∠F=90°,再利用AAS证明△ABE≌△FDE即可.
点评:此题主要考查了图形的翻折变换,以及矩形的性质,关键是掌握矩形的对边相等,四个角都是90°.
∵∠CBD=25°,
∴∠FBD=25°,
∵四边形ABCD是矩形,

∴AD∥BC,
∴∠AEB=∠EBC=25°+25°=50°;
(2)根据折叠可得:DF=AB,∠F=∠C=90°,
∵四边形ABCD是矩形,
∴AB=CD=FD,∠A=∠C=∠F=90°,
∵在△AEB和△FED中,
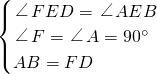 ,
,∴△ABE≌△FDE(AAS).
分析:(1)根据折叠可得∠FBD=∠DBC,进而可得到∠FBD=25°,再根据两直线平行,内错角相等可得∠AEB的度数;
(2)根据折叠可得:DF=AB,∠F=∠C=90°,根据矩形的性质可得AB=CD=FD,∠A=∠C=∠F=90°,再利用AAS证明△ABE≌△FDE即可.
点评:此题主要考查了图形的翻折变换,以及矩形的性质,关键是掌握矩形的对边相等,四个角都是90°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4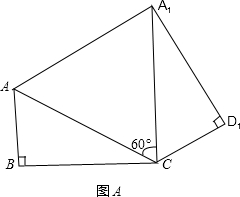
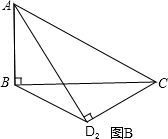
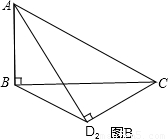
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.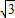 ,将矩形沿对角线AC剪开,解答以下问题:
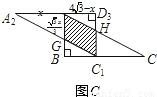
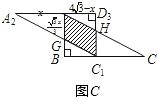
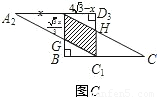
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.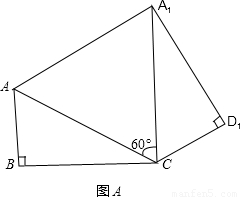



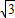 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: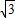 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.