题目内容
【题目】如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连结OD,AC.
(1)求证:∠B=∠DCA;
(2)若 ![]() ,OD=
,OD= ![]() , 求⊙O的半径长.
, 求⊙O的半径长.
【答案】
(1)解:连接 ![]() ,
, ![]() 与
与 ![]() 相切,
相切,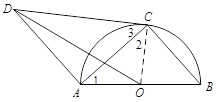
![]()
![]() 是
是 ![]() 的直径,
的直径, ![]()
![]()
![]()
![]()
![]() 即
即 ![]()
(2)解: ![]() ,
, ![]() 是
是 ![]() 的直径,
的直径, ![]()
![]()
![]()
![]()
![]()
![]()
![]() 设
设 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在
在 ![]() 中,
中, ![]()
![]() ,解得
,解得 ![]()
![]() 的半径长为3
的半径长为3
【解析】(1)根据切线的性质可得![]() DCO=
DCO=![]() ,由直径所对的圆周角是直角可得∠ A C B =
,由直径所对的圆周角是直角可得∠ A C B = ![]() ,再结合已知条件结论可得;(2)根据已知条件可证△ABC△DCA,则DC可表示出来,在 △ O D C 中,用勾股定理可求解。
,再结合已知条件结论可得;(2)根据已知条件可证△ABC△DCA,则DC可表示出来,在 △ O D C 中,用勾股定理可求解。
【考点精析】关于本题考查的勾股定理的概念和圆周角定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目



