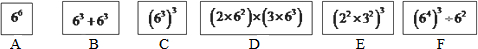题目内容

阅读材料：
1
2
+1
=
1×(
2
-1)
(
2
+1)(
2
-1)
=
2
-1；
1
3
+
2
=
3
-
2
(
3
+
2
)(
3
-
2
)
=
3
-
2
；
1
5
+2
=
5
-2
(
5
+2)(
5
-2)
=
5
-2
…
按照上述式子变形的思路求：
（1）
1
7
+
6
；
（2）
1
n+1
+
n
（n为正整数）
（3）根据你发现的规律，请计算：(
1
1+
2
+
1
3
+
2
+
1
4
+
3
+…+
1
2010
+
2009
+
1
2011
+
2010
)(1+
2011
)．
考点：分母有理化
专题：规律型
分析：（1）利用已知将分子与分母同乘以（
7
-
6
）得出即可；
（2）利用已知将分子与分母同乘以（
n+1
-
n
）得出即可；
（3）利用（1）中所求规律进而化简求出即可．
解答：解：（1）
1
7
+
6
=
7
-
6
(
7
+
6
)×(
7
-
6
)
=
7
-
6
；

（2）
1
n+1
+
n
=
n+1
-
n
(
n+1
+
n
)(
n+1
-
n
)
=
n+1
-
n
；

（3）(
1
1+
2
+
1
3
+
2
+
1
4
+
3
+…+
1
2010
+
2009
+
1
2011
+
2010
)(1+
2011
)
=（
2
-1+
3
-
2
+
4
-
3
+…+
2011
-
2010
）×（1+
2011
）
=（
2011
-1）×（1+
2011
）
=2011-1
=2010．
点评：此题主要考查了分母有理化，正确化简二次根式是解题关键．
练习册系列答案
相关题目
先化简，再求值：(a-1+
2
a+1
)÷(a2+1)，其中a=cos45°-1．
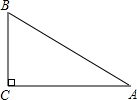如图，已知在Rt△ABC中，∠C=90°，BC=2，∠A=30°，求AC．
平行四边形ABCD中，BG垂直于CD，且AB=BG=BE，AE交BG于点F． 
（1）若AB=3，∠BAD=60°，求CE的长；
（2）求证：AD=BF+CG．
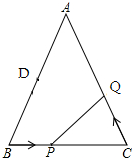如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
（1）若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由；
（2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
已知 10m=0.2，10n=4，求：
（1）2m-n的值；
（2）9m÷3n的值．
画图并计算：已知线段AB=10cm．
（1）在线段AB上画线段BC=4cm，求线段AC的长；
（2）在直线AB上画线段BC=4cm，求线段AC的长．
一次数学兴趣小组活动中，同学们做了一个找朋友的游戏：有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面，如图，A、B、C、D、E、F所持的纸牌的前面分别写有六个算式：66；63+63；（63）3；（2×62）×（3×63）；（22×32）3；（64）3÷62．游戏规定：所持算式的值相等的两个人是朋友．如果现在由同学A来找他的朋友，他可以找谁呢？说说你的看法．
一次函数y=2x+m的截距为-4，这个函数解析式是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网