题目内容
【题目】如图![]() ,点C为△ABD外接圆上的一动点(点C不在
,点C为△ABD外接圆上的一动点(点C不在![]() 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:![]() AC=BC+CD;
AC=BC+CD;
(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究![]() ,
,![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.

【答案】(1)详见解析;(2)详见解析;(3)DM2=BM2+2MA2,理由详见解析.
【解析】
试题分析:(1)易证△ABD为等腰直角三角形,即可判定BD是该外接圆的直径;(2)如图所示作CA⊥AE,延长CB交AE于点E,再证△ACE为等腰直角三角形,可得AC=AE,再由勾股定理即可得![]() ;利用SAS判定△ABE≌△ADC,可得BE=DC,所以CE=BE+B,所以C=DC+BC=
;利用SAS判定△ABE≌△ADC,可得BE=DC,所以CE=BE+B,所以C=DC+BC=![]() ;(3)延长MB交圆于点E,连结AE、DE,因∠BEA=∠ACB=∠BMA=45°,在△MAE中有MA=AE,∠MAE=90°,由勾股定理可得
;(3)延长MB交圆于点E,连结AE、DE,因∠BEA=∠ACB=∠BMA=45°,在△MAE中有MA=AE,∠MAE=90°,由勾股定理可得![]() ,再证∠BED=90°,在RT△MED中,有
,再证∠BED=90°,在RT△MED中,有![]() ,所以
,所以![]() .
.
试题解析:(1)∵弧AB=弧AB, ∴∠ADB=∠ACB
又∵∠ACB=∠ABD=45° ∴∠ABD=∠ADB=45°
∴∠BAD=90° ∴△ABD为等腰直角三角形
∴BD是该外接圆的直径
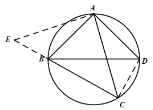
(2)如图所示作CA⊥AE,延长CB交AE于点E
∵∠ACB=45°,CA⊥AE
∴△ACE为等腰直角三角形 ∴AC=AE
由勾股定理可知CE2=AC2+AE2=2AC2 ∴![]()
由(1)可知△ABD 为等腰直角三角形
∴AB=AD ∠BAD=90° 又∵∠EAC=90°
∴∠EAB+∠BAC=∠DAC+∠BAC ∴∠EAB=∠DAC
∴在△ABE和△ADC中
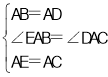
∴△ABE≌△ADC(SAS)
∴BE=DC
∴CE=BE+BC=DC+BC=![]()
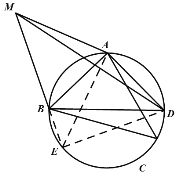
(3)DM2=BM2+2MA2
延长MB交圆于点E,连结AE、DE
∵∠BEA=∠ACB=∠BMA=45°
∴在△MAE中有MA=AE,∠MAE=90°
∴![]()
又∵AC=MA=AE
∴![]() =
=![]()
又∵![]() =
=![]()
∴![]() -
-![]() +
+![]() =
=![]() -
-![]() +
+![]()
即![]() =
=![]()
∴DE=BC=MB
∵BD为直径
∴∠BED=90°
在RT△MED中,有![]()
∴![]()


 单元期中期末卷系列答案
单元期中期末卷系列答案

