题目内容
已知方程x2-2x-5=0,有下列判断:①x1+x2=-2;②x1•x2=-5;③方程有实数根;④方程没有实数根;则下列选项正确的是
- A.①②
- B.①②③
- C.②③
- D.①②④
C
分析:先根据一元二次方程x2-2x-5=0得出a、b、c的值,再根据根与系数的关系得出x1+x2;x1•x2的值,由△的值判断出方程根的情况即可.
解答:∵方程x2-2x-5=0中,a=1,b=-2,c=-5,
∴x1+x2=-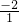 =2,x1•x2=
=2,x1•x2= =-5,故①错误;②正确;
=-5,故①错误;②正确;
∵方程x2-2x-5=0中,△=(-2)2-4×(-5)=4+20=24>0,
∴方程有实数根,故③正确,④错误.
故选C.
点评:本题考查的是根的判别式及根与系数的关系,熟知一元二次方程ax2+bx+c=0(a≠0)中,当△>0时,方程有两个不相等的两个实数根;x1+x2=- ,x1x2=
,x1x2= 的知识是解答此题的关键.
的知识是解答此题的关键.
分析:先根据一元二次方程x2-2x-5=0得出a、b、c的值,再根据根与系数的关系得出x1+x2;x1•x2的值,由△的值判断出方程根的情况即可.
解答:∵方程x2-2x-5=0中,a=1,b=-2,c=-5,
∴x1+x2=-
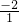 =2,x1•x2=
=2,x1•x2= =-5,故①错误;②正确;
=-5,故①错误;②正确;∵方程x2-2x-5=0中,△=(-2)2-4×(-5)=4+20=24>0,
∴方程有实数根,故③正确,④错误.
故选C.
点评:本题考查的是根的判别式及根与系数的关系,熟知一元二次方程ax2+bx+c=0(a≠0)中,当△>0时,方程有两个不相等的两个实数根;x1+x2=-
 ,x1x2=
,x1x2= 的知识是解答此题的关键.
的知识是解答此题的关键. 
练习册系列答案
相关题目