题目内容
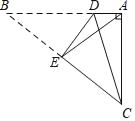
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.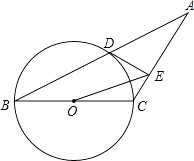
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
【答案】
(1)证明:连接OD,CD,
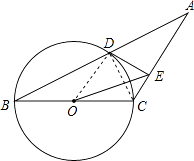
∵BC为⊙O直径,
∴∠BDC=90°,
即CD⊥AB,
∵△ABC是等腰三角形,
∴AD=BD,
∵OB=OC,
∴OD是△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵D点在⊙O上,
∴DE为⊙O的切线;
(2)解:∵∠A=∠B=30°,BC=4,
∴CD= ![]() BC=2,BD=BCcos30°=2
BC=2,BD=BCcos30°=2 ![]() ,
,
∴AD=BD=2 ![]() ,AB=2BD=4
,AB=2BD=4 ![]() ,
,
∴S△ABC= ![]() ABCD=
ABCD= ![]() ×4
×4 ![]() ×2=4
×2=4 ![]() ,
,
∵DE⊥AC,
∴DE= ![]() AD=
AD= ![]() ×2
×2 ![]() =
= ![]() ,
,
AE=ADcos30°=3,
∴S△ODE= ![]() ODDE=
ODDE= ![]() ×2×
×2× ![]() =
= ![]() ,
,
S△ADE= ![]() AEDE=
AEDE= ![]() ×
× ![]() ×3=
×3= ![]() ,
,
∵S△BOD= ![]() S△BCD=
S△BCD= ![]() ×
× ![]() S△ABC=
S△ABC= ![]() ×4
×4 ![]() =
= ![]() ,
,
∴S△OEC=S△ABC﹣S△BOD﹣S△ODE﹣S△ADE=4 ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() .
.
【解析】(1)证DE为⊙O的切线,就得证DE垂直过D点的半径,为此连接OD、CD,可证出OD是△ABC的中位线可得OD∥AC,由已知可得证;
(2)结合图形可知,S△OEC=S△ABC﹣S△BOD﹣S△ODE﹣S△ADE,所以先求出S△ABC、S△BOD、S△ODE、S△ADE,为此利用三角函数的性质求出BD、DE、AE的长,继而求得答案.

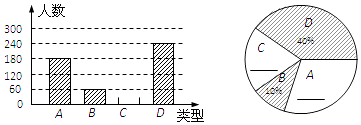
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.
课外阅读时间频数分布表
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
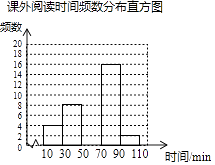
请根据图表中提供的信息回答下列问题:
(1)a= , b=;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?