Question

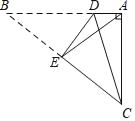
【题目】如图，Rt△ABC中，∠BAC＝90°，AC＝9，AB＝12．按如图所示方式折叠，使点B、C重合，折痕为DE，连接AE．求AE与CD的长．

Answer 1

【答案】AE＝7.5，CD＝

【解析】

在Rt△ABC中由于∠BAC＝90°，AC＝9，AB＝12，所以根据勾股定理可求出BC的长，由折叠可知，ED垂直平分BC，E为BC中点，BD＝CD，根据直角三角形斜边上的中线等于斜边的一半可求出AE的长，设BD＝CD＝x，则AD＝12﹣x．在Rt△ADC中由AD2+AC 2＝CD2即可求出x的值，故可得出结论．

解：在Rt△ABC中，∠BAC＝90°，AC＝9，AB＝12，

由勾股定理得：AB2+AC 2＝BC2．

∴BC2＝92+122＝81+144＝225＝152，

∴BC＝15

∵由折叠可知，ED垂直平分BC，

∴E为BC中点，BD＝CD

∴AE＝BC＝7.5 （直角三角形斜边上的中线等于斜边的一半）．

设BD＝CD＝x，则AD＝12﹣x．

在Rt△ADC中，

∴AD2+AC 2＝CD2 （勾股定理）．

即92+（12﹣x）2＝x2，解得x＝，

∴CD＝．