题目内容
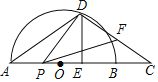
【题目】如图,⊙O的半径为5,△ABC是⊙O的内接三角形,AB=8.AD和过点B的切线互相垂直,垂足为D.
(1)求证:∠BAD+∠C=90°;
(2)求线段AD的长.
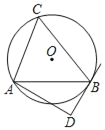
【答案】(1)证明见解析;(2)6.4
【解析】
(1)连接BO延长交⊙O于E,连接AE,根据切线的性质、结合题意得到AD∥BE,根据平行线的性质、圆周角定理证明;
(2)证明△ABE∽△DAB,根据相似三角形的性质得到比例式,计算即可.
(1)连接BO延长交⊙O于E,连接AE,
∵DB为⊙O的切线,
∴EB⊥BD,
∵AD⊥BD,
∴AD∥BE,
∴∠BAD=∠EBA,
∵BE为直径,
∴∠EBA+∠E=90°,
由圆周角定理得,∠E=∠C,
∴∠BAD+∠C=90°;
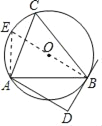
(2)∵⊙O的半径为5,
∴BE=10.
∵∠BAD=∠EBA,∠D=∠BAE,
∴△ABE∽△DAB,
∴![]() ,
,
∵AB=8,BE=10,
∴AD=6.4,
∴线段AD的长度为6.4.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目