ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐΆΦœσΒΡΕΞΒψΉχ±ξΈΣΘ®0Θ§1Θ©Θ§«“ΙΐΒψΘ®©¹1Θ§ ![]() Θ©Θ§÷±œΏy=kx+2”κy÷αœύΫΜ”ΎΒψPΘ§”κΕΰ¥ΈΚ· ΐΆΦœσΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ®x1 Θ§ y1Θ©Θ§BΘ®x2 Θ§ y2Θ©Θ° Θ®ΉΔΘΚ‘ΎΫβΧβΙΐ≥Χ÷–Θ§Ρψ“≤Ω…“‘‘ΡΕΝΚσΟφΒΡ≤ΡΝœΘ©
Θ©Θ§÷±œΏy=kx+2”κy÷αœύΫΜ”ΎΒψPΘ§”κΕΰ¥ΈΚ· ΐΆΦœσΫΜ”Ύ≤ΜΆ§ΒΡΝΫΒψAΘ®x1 Θ§ y1Θ©Θ§BΘ®x2 Θ§ y2Θ©Θ° Θ®ΉΔΘΚ‘ΎΫβΧβΙΐ≥Χ÷–Θ§Ρψ“≤Ω…“‘‘ΡΕΝΚσΟφΒΡ≤ΡΝœΘ©
ΗΫΘΚ‘ΡΕΝ≤ΡΝœ
»ΈΚΈ“ΜΗω“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυ”κœΒ ΐΒΡΙΊœΒΈΣΘΚΝΫΗυΒΡΚΆΒ»”Ύ“Μ¥ΈœνœΒ ΐ”κΕΰ¥ΈœνœΒ ΐΒΡ±»ΒΡœύΖ¥ ΐΘ§ΝΫΗυΒΡΜΐΒ»”Ύ≥Θ ΐœν”κΕΰ¥ΈœνœΒ ΐΒΡ±»Θ°
Φ¥ΘΚ…η“Μ‘ΣΕΰ¥ΈΖΫ≥Χax2+bx+c=0ΒΡΝΫΗυΈΣx1 Θ§ x2 Θ§
‘ρΘΚx1+x2=©¹ ![]() Θ§x1x2=
Θ§x1x2= ![]()
ΡήΝιΜν‘Υ”Ο’β÷÷ΙΊœΒΘ§”– ±Ω…“‘ ΙΫβΧβΗϋΈΣΦρΒΞΘ°
άΐΘΚ≤ΜΫβΖΫ≥ΧΘ§«σΖΫ≥Χx2©¹3x=15ΝΫΗυΒΡΚΆ”κΜΐΘ°
ΫβΘΚ‘≠ΖΫ≥Χ±δΈΣΘΚx2©¹3x©¹15=0
ΓΏ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΗυ”κœΒ ΐ”–ΙΊœΒΘΚx1+x2=©¹ ![]() Θ§x1x2=
Θ§x1x2= ![]()
Γύ‘≠ΖΫ≥ΧΝΫΗυ÷°ΚΆ=©¹ ![]() =3Θ§ΝΫΗυ÷°Μΐ=
=3Θ§ΝΫΗυ÷°Μΐ= ![]() =©¹15Θ°
=©¹15Θ°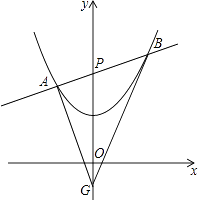
Θ®1Θ©«σΗΟΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ°
Θ®2Θ©Ε‘Θ®1Θ©÷–ΒΡΕΰ¥ΈΚ· ΐΘ§Β±Ή‘±δΝΩx»Γ÷ΒΖΕΈß‘Ύ©¹1ΘΦxΘΦ3 ±Θ§«κ–¥≥ωΤδΚ· ΐ÷ΒyΒΡ»Γ÷ΒΖΕΈßΘΜΘ®≤Μ±ΊΥΒΟςάμ”…Θ©
Θ®3Θ©«σ÷ΛΘΚ‘Ύ¥ΥΕΰ¥ΈΚ· ΐΆΦœσœ¬ΖΫΒΡy÷α…œΘ§±Ί¥φ‘ΎΕ®ΒψGΘ§ ΙΓςABGΒΡΡΎ«–‘≤ΒΡ‘≤–Ρ¬δ‘Ύy÷α…œΘ§≤Δ«σΓςGABΟφΜΐΒΡΉν–Γ÷ΒΘ°
ΓΨ¥πΑΗΓΩ
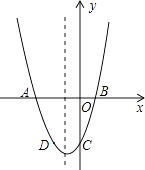
Θ®1Θ©ΫβΘΚ”…”ΎΕΰ¥ΈΚ· ΐΆΦœσΒΡΕΞΒψΉχ±ξΈΣΘ®0Θ§1Θ©Θ§
“ρ¥ΥΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΩ……ηΈΣy=ax2+1Θ°
ΓΏ≈ΉΈοœΏy=ax2+1ΙΐΒψΘ®©¹1Θ§ ![]() Θ©Θ§
Θ©Θ§
Γύ ![]() =a+1Θ°
=a+1Θ°
ΫβΒΟΘΚa= ![]() Θ°
Θ°
ΓύΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣΘΚy= ![]() x2+1
x2+1
Θ®2Θ©ΫβΘΚΒ±x=©¹1 ±Θ§y= ![]() Θ§
Θ§
Β±x=0 ±Θ§y=1Θ§
Β±x=3 ±Θ§y= ![]() ΓΝ32+1=
ΓΝ32+1= ![]() Θ§
Θ§
ΫαΚœΆΦ1Ω…ΒΟΘΚΒ±©¹1ΘΦxΘΦ3 ±Θ§yΒΡ»Γ÷ΒΖΕΈß «1ΓήyΘΦ ![]()
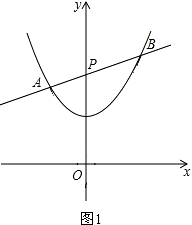
Θ®3Θ©ΔΌ÷ΛΟςΘΚΙΐΒψAΉςy÷αΒΡΕ‘≥ΤΒψAΓδΘ§Ν§Ϋ”BAΓδ≤Δ―”≥ΛΘ§ΫΜy÷α”ΎΒψGΘ§Ν§Ϋ”AGΘ§»γΆΦ2Θ§
‘ρΒψAΓδ±Ί‘Ύ≈ΉΈοœΏ…œΘ§«“ΓœAGP=ΓœBGPΘ§
ΓύΓςABGΒΡΡΎ«–‘≤ΒΡ‘≤–Ρ¬δ‘Ύy÷α…œΘ°
ΓΏΒψAΒΡΉχ±ξΈΣΘ®x1Θ§y1Θ©Θ§
ΓύΒψAΓδΒΡΉχ±ξΈΣΘ®©¹x1Θ§y1Θ©Θ°
ΓΏΒψAΘ®x1Θ§y1Θ©ΓΔBΘ®x2Θ§y2Θ©‘Ύ÷±œΏy=kx+2…œΘ§
Γύy1=kx1+2Θ§y2=kx2+2Θ°
ΓύΒψAΓδΒΡΉχ±ξΈΣΘ®©¹x1Θ§kx1+2Θ©ΓΔΒψBΒΡΉχ±ξΈΣΘ®x2Θ§kx2+2Θ©Θ°
…η÷±œΏBGΒΡΫβΈω ΫΈΣy=mx+nΘ§‘ρΒψGΒΡΉχ±ξΈΣΘ®0Θ§nΘ©Θ°
ΓΏΒψAΓδΘ®©¹x1Θ§kx1+2Θ©ΓΔBΘ®x2Θ§kx2+2Θ©‘Ύ÷±œΏBG…œΘ§
Γύ ![]() Θ°
Θ°
ΫβΒΟΘΚ 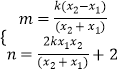 Θ°
Θ°
ΓΏAΘ®x1Θ§y1Θ©Θ§BΘ®x2Θ§y2Θ© «÷±œΏy=kx+2”κ≈ΉΈοœΏy= ![]() x2+1ΒΡΫΜΒψΘ§
x2+1ΒΡΫΜΒψΘ§
Γύx1ΓΔx2 «ΖΫ≥Χkx+2= ![]() x2+1Φ¥x2©¹4kx©¹4=0ΒΡΝΫΗω Β ΐΗυΘ°
x2+1Φ¥x2©¹4kx©¹4=0ΒΡΝΫΗω Β ΐΗυΘ°
Γύ”…Ηυ”κœΒ ΐΒΡΙΊœΒΩ…ΒΟΘΜx1+x2=4kΘ§x1x2=©¹4Θ°
Γύn= ![]() =©¹2+2=0Θ°
=©¹2+2=0Θ°
ΓύΒψGΒΡΉχ±ξΈΣΘ®0Θ§0Θ©Θ°
Γύ‘Ύ¥ΥΕΰ¥ΈΚ· ΐΆΦœσœ¬ΖΫΒΡy÷α…œΘ§¥φ‘ΎΕ®ΒψGΘ®0Θ§0Θ©Θ§ ΙΓςABGΒΡΡΎ«–‘≤ΒΡ‘≤–Ρ¬δ‘Ύy÷α…œΘ°
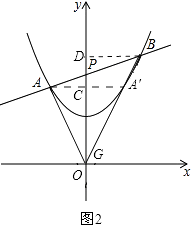
ΔΎΫβΘΚΙΐΒψAΉςACΓΆOPΘ§¥ΙΉψΈΣCΘ§ΙΐΒψBΉςBDΓΆOPΘ§¥ΙΉψΈΣDΘ§»γΆΦ2Θ§

ΓΏ÷±œΏy=kx+2”κy÷αœύΫΜ”ΎΒψPΘ§
ΓύΒψPΒΡΉχ±ξΈΣΘ®0Θ§2Θ©Θ°
ΓύPG=2Θ°
ΓύSΓςABG=SΓςAPG+SΓςBPG
= ![]() PGAC+
PGAC+ ![]() PGBD
PGBD
= ![]() PGΘ®AC+BDΘ©
PGΘ®AC+BDΘ©
= ![]() ΓΝ2ΓΝΘ®©¹x1+x2Θ©
ΓΝ2ΓΝΘ®©¹x1+x2Θ©
=x2©¹x1
= ![]()
= ![]()
= ![]()
=4 ![]() Θ°
Θ°
ΓύΒ±k=0 ±Θ§SΓςABGΉν–ΓΘ§Ήν–Γ÷ΒΈΣ4Θ°
ΓύΓςGABΟφΜΐΒΡΉν–Γ÷ΒΈΣ4Θ°
ΓΨΫβΈωΓΩΘ®1Θ©…ηΕΰ¥ΈΚ· ΐΫβΈω ΫΈΣy=ax2+1Θ§”…”ΎΒψΘ®©¹1Θ§ ![]() Θ©‘ΎΕΰ¥ΈΚ· ΐΆΦœσ…œΘ§Α―ΗΟΒψΒΡΉχ±ξ¥ζ»κy=ax2+1Θ§Φ¥Ω…«σ≥ωaΘ§¥”Εχ«σ≥ωΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ°Θ®2Θ©œ»Ζ÷±π«σ≥ωx=©¹1Θ§x=0Θ§x=3 ±yΒΡ÷ΒΘ§»ΜΚσΫαΚœΆΦœσΨΆΩ…ΒΟΒΫyΒΡ»Γ÷ΒΖΕΈßΘ°Θ®3Θ©ΙΐΒψAΉςy÷αΒΡΕ‘≥ΤΒψAΓδΘ§Ν§Ϋ”BAΓδ≤Δ―”≥ΛΘ§ΫΜy÷α”ΎΒψGΘ§Ν§Ϋ”AGΘ§»γΆΦ2Θ§‘ρΒψAΓδ±Ί‘Ύ≈ΉΈοœΏ…œΘ§«“ΓœAGP=ΓœBGPΘ§”…¥ΥΩ…ΒΟΓςABGΒΡΡΎ«–‘≤ΒΡ‘≤–Ρ¬δ‘Ύy÷α…œΘ°”…”ΎΒψAΘ®x1 Θ§ y1Θ©ΓΔBΘ®x2 Θ§ y2Θ©‘Ύ÷±œΏy=kx+2…œΘ§¥”ΕχΩ…“‘ΒΟΒΫΒψAΒΡΉχ±ξΈΣΘ®x1 Θ§ kx1+2Θ©ΓΔAΓδΒΡΉχ±ξΈΣΘ®©¹x1 Θ§ kx1+2Θ©ΓΔBΒΡΉχ±ξΈΣΘ®x2 Θ§ kx2+2Θ©Θ°…η÷±œΏBGΒΡΫβΈω ΫΈΣy=mx+nΘ§‘ρΒψGΒΡΉχ±ξΈΣΘ®0Θ§nΘ©Θ°”…”ΎΒψAΓδΘ®©¹x1 Θ§ kx1+2Θ©ΓΔBΘ®x2 Θ§ kx2+2Θ©‘Ύ÷±œΏBG…œΘ§Ω…”ΟΚ§”–kΓΔx1ΓΔx2ΒΡ¥ζ ΐ Ϋ±μ ΨnΘ°”…”ΎAΓΔB «÷±œΏy=kx+2”κ≈ΉΈοœΏy=
Θ©‘ΎΕΰ¥ΈΚ· ΐΆΦœσ…œΘ§Α―ΗΟΒψΒΡΉχ±ξ¥ζ»κy=ax2+1Θ§Φ¥Ω…«σ≥ωaΘ§¥”Εχ«σ≥ωΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΘ°Θ®2Θ©œ»Ζ÷±π«σ≥ωx=©¹1Θ§x=0Θ§x=3 ±yΒΡ÷ΒΘ§»ΜΚσΫαΚœΆΦœσΨΆΩ…ΒΟΒΫyΒΡ»Γ÷ΒΖΕΈßΘ°Θ®3Θ©ΙΐΒψAΉςy÷αΒΡΕ‘≥ΤΒψAΓδΘ§Ν§Ϋ”BAΓδ≤Δ―”≥ΛΘ§ΫΜy÷α”ΎΒψGΘ§Ν§Ϋ”AGΘ§»γΆΦ2Θ§‘ρΒψAΓδ±Ί‘Ύ≈ΉΈοœΏ…œΘ§«“ΓœAGP=ΓœBGPΘ§”…¥ΥΩ…ΒΟΓςABGΒΡΡΎ«–‘≤ΒΡ‘≤–Ρ¬δ‘Ύy÷α…œΘ°”…”ΎΒψAΘ®x1 Θ§ y1Θ©ΓΔBΘ®x2 Θ§ y2Θ©‘Ύ÷±œΏy=kx+2…œΘ§¥”ΕχΩ…“‘ΒΟΒΫΒψAΒΡΉχ±ξΈΣΘ®x1 Θ§ kx1+2Θ©ΓΔAΓδΒΡΉχ±ξΈΣΘ®©¹x1 Θ§ kx1+2Θ©ΓΔBΒΡΉχ±ξΈΣΘ®x2 Θ§ kx2+2Θ©Θ°…η÷±œΏBGΒΡΫβΈω ΫΈΣy=mx+nΘ§‘ρΒψGΒΡΉχ±ξΈΣΘ®0Θ§nΘ©Θ°”…”ΎΒψAΓδΘ®©¹x1 Θ§ kx1+2Θ©ΓΔBΘ®x2 Θ§ kx2+2Θ©‘Ύ÷±œΏBG…œΘ§Ω…”ΟΚ§”–kΓΔx1ΓΔx2ΒΡ¥ζ ΐ Ϋ±μ ΨnΘ°”…”ΎAΓΔB «÷±œΏy=kx+2”κ≈ΉΈοœΏy= ![]() x2+1ΒΡΫΜΒψΘ§”…Ηυ”κœΒ ΐΒΡΙΊœΒΩ…ΒΟΘΚx1+x2=4kΘ§x1x2=©¹4Θ°¥”Εχ«σ≥ωn=0Θ§Φ¥Ω…÷Λ≥ωΘΚ‘Ύ¥ΥΕΰ¥ΈΚ· ΐΆΦœσœ¬ΖΫΒΡy÷α…œΘ§¥φ‘ΎΕ®ΒψGΘ®0Θ§0Θ©Θ§ ΙΓςABGΒΡΡΎ«–‘≤ΒΡ‘≤–Ρ¬δ‘Ύy÷α…œΘ°”…SΓςABG=SΓςAPG+SΓςBPG Θ§ Ω…“‘ΒΟΒΫSΓςABG=x2©¹x1=
x2+1ΒΡΫΜΒψΘ§”…Ηυ”κœΒ ΐΒΡΙΊœΒΩ…ΒΟΘΚx1+x2=4kΘ§x1x2=©¹4Θ°¥”Εχ«σ≥ωn=0Θ§Φ¥Ω…÷Λ≥ωΘΚ‘Ύ¥ΥΕΰ¥ΈΚ· ΐΆΦœσœ¬ΖΫΒΡy÷α…œΘ§¥φ‘ΎΕ®ΒψGΘ®0Θ§0Θ©Θ§ ΙΓςABGΒΡΡΎ«–‘≤ΒΡ‘≤–Ρ¬δ‘Ύy÷α…œΘ°”…SΓςABG=SΓςAPG+SΓςBPG Θ§ Ω…“‘ΒΟΒΫSΓςABG=x2©¹x1= ![]() =4
=4 ![]() Θ§Υυ“‘Β±k=0 ±Θ§SΓςABGΉν–ΓΘ§Ήν–Γ÷ΒΈΣ4Θ°
Θ§Υυ“‘Β±k=0 ±Θ§SΓςABGΉν–ΓΘ§Ήν–Γ÷ΒΈΣ4Θ°
ΓΨΩΦΒψΨΪΈωΓΩ»œ’φ…σΧβΘ§ Ήœ»–η“ΣΝΥΫβΗυ”κœΒ ΐΒΡΙΊœΒ(“Μ‘ΣΕΰ¥ΈΖΫ≥Χax2+bx+c=0Θ®aΓΌ0Θ©ΒΡΗυ”…ΖΫ≥ΧΒΡœΒ ΐaΓΔbΓΔcΕχΕ®ΘΜΝΫΗυ÷°ΚΆΒ»”ΎΖΫ≥ΧΒΡ“Μ¥ΈœνœΒ ΐ≥ΐ“‘Εΰ¥ΈœνœΒ ΐΥυΒΟΒΡ…ΧΒΡœύΖ¥ ΐΘΜΝΫΗυ÷°ΜΐΒ»”Ύ≥Θ ΐœν≥ΐ“‘Εΰ¥ΈœνœΒ ΐΥυΒΟΒΡ…Χ)Θ§ΜΙ“Σ’ΤΈ’»ΖΕ®“Μ¥ΈΚ· ΐΒΡ±μ¥ο Ϋ(»ΖΕ®“ΜΗω“Μ¥ΈΚ· ΐΘ§–η“Σ»ΖΕ®“Μ¥ΈΚ· ΐΕ®“ε Ϋy=kx+bΘ®k≤ΜΒ»”Ύ0Θ©÷–ΒΡ≥Θ ΐkΚΆbΘ°Ϋβ’βάύΈ ΧβΒΡ“ΜΑψΖΫΖ® «¥ΐΕ®œΒ ΐΖ®)ΒΡœύΙΊ÷Σ Ε≤≈ «¥πΧβΒΡΙΊΦϋΘ°

ΓΨΧβΡΩΓΩ“ΜΈΜ…δΜς‘ΥΕ·‘±‘Ύ10¥Έ…δΜς―ΒΝΖ÷–Θ§Οϋ÷–Α–ΒΡΜΖ ΐ»γΆΦΘ° «κΡψΗυΨίΆΦ±μΘ§Άξ≥…œ¬Ν–Έ ΧβΘΚ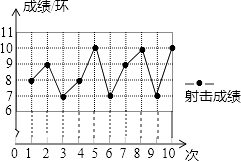
Θ®1Θ©≤Ι≥δΆξ≥…œ¬Οφ≥…Φ®±μΒΞΒΡΧν–¥ΘΚ
…δΜς–ρ¥Έ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
≥…Φ®/ΜΖ | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
Θ®2Θ©«σΗΟ‘ΥΕ·‘±’β10¥Έ…δΜς―ΒΝΖΒΡΤΫΨυ≥…Φ®Θ°