题目内容
【题目】已知∠AOB＝60°，自O点引射线OC，若∠AOC：∠COB＝2：3，求OC与∠AOB的平分线所成的角的度数．
【答案】6°或150°．
【解析】
设OD是∠AOB的平分线，分两种情况进行讨论：①OC在∠AOB内部，利用∠COD＝∠AOD﹣∠AOC求解；②OC在∠AOB外部，利用∠COD＝∠AOC+∠AOD，即可求解．
设OD是∠AOB的平分线，分两种情况：
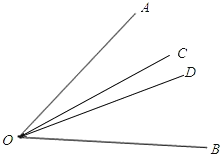
①若OC在∠AOB内部，
∵∠AOC：∠COB＝2：3，
∴设∠AOC＝2x，∠COB＝3x，
∵∠AOB＝60°，
∴2x+3x＝60°，
解得：x＝12°，
∴∠AOC＝2x＝2×12°＝24°，∠COB＝3x＝3×12°＝36°，
∵OD平分∠AOB，
∴∠AOD＝30°，
∴∠COD＝∠AOD﹣∠AOC＝30°﹣24°＝6°；
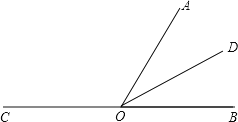
②若OC在∠AOB外部，
∵∠AOC：∠COB＝2：3，
∴设∠AOC＝2x，∠COB＝3x，
∵∠AOB＝60°，
∴3x﹣2x＝60°，
解得：x＝60°，
∴∠AOC＝2x＝2×60°＝120°，∠COB＝3x＝3×60°＝180°，
∵OD平分∠AOB，
∴∠AOD＝30°，
∴∠COD＝∠AOC+∠AOD＝120°+30°＝150°．
∴OC与∠AOB的平分线所成的角的度数为6°或150°．
练习册系列答案
名校课堂系列答案
相关题目
