题目内容
【题目】 如图,正方形ABCD中,E是AD的中点,F是AB边上的一点,连接FE并延长与CD的延长线相交于点G,作EH⊥FG交BC的延长线于点H.
(1)若BC=8,BF=5,求线段FG的长;
(2)求证:EH=2EG.

【答案】(1)10;(2)证明见解析.
【解析】试题分析:
试题解析:(1)∵BC=8,BF=5
∴AF=3
∵E是AD的中点,
∴AE=4
在△AFE中,EF=![]() =5,
=5,
∵四边形ABCD是正方形,
∴∠A=∠EDG=90°,
∵E为AD中点,
∴AE=ED,
在△AFE和△DGE中
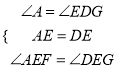
∴△AFE≌△DGE(ASA),
∴EF=EG,
∴FG=2EF=10;
(2)证明:过E作EM⊥BH于M,过G作GN⊥BA交BA的延长线于点N,
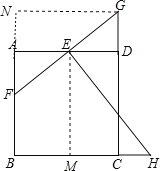
∵EH⊥FG,
∴∠HEG=90°,
∴∠H=∠FEM,
∵四边形ABCD是正方形,
∴∠DCB=90°,
∵EM⊥BC,
∴EM∥CD,
∴∠EGC=∠FEM,
∴∠H=∠EGC,
∵AB∥CD,
∴∠EGC=∠NFG
∴∠H=∠NFG,
在△NFG与△MHE中,
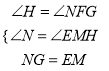
∴△NFG≌△MHE(AAS)
∴EH=FG=2EG.

练习册系列答案
相关题目
