题目内容
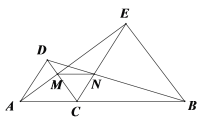
【题目】如图,点C在AB上,△DAC、△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,则下列结论:①AE=DB;②CM=CN;③△CMN为等边三角形;④MN//BC;
正确的有_________(填序号)
【答案】①②③④
【解析】
试题解析:∵△ACD和△BCE为等边三角形,
∴AC=DC,BC=EC,∠ACD=∠ECB=60°,
∴∠ACE=∠BCD,
在△ACE和△DCB中

∴△ACE≌△DCB(SAS),
∴AE=BD,
∵△ACE≌△DCB,
∴∠MAC=∠NDC,
∵∠ACD=∠BCE=60°,
∴∠MCA=∠DCN=60°,
在△AMC和△DNC中
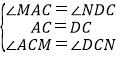
∴△AMC≌△DNC(ASA),
∴CM=CN,
∴△CMN为等边三角形,
∴∠NMC=∠NCB=60°,
∴MN∥BC.
故正确的有①②③④.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目


