题目内容
24、如图，△ABC绕点B逆时针方向旋转到△EBD的位置．若∠A=15°、∠C=10°，E、B、C在同一直线上，则∠ABC为多少度？旋转角度是？
分析：在△ABC中，已知∠A=15°、∠C=10°，根据内角和定理可求∠ABC；点B为旋转中心，E的对应点为A，故旋转角为∠ABE，由互补关系可求∠ABE．
解答：解：在△ABC中，已知∠A=15°，∠C=10°，
∴∠ABC=180°-∠A-∠C=155°；
又∵点B为旋转中心，E的对应点为A，
∴旋转角为∠ABE=180°-∠ABC=25°．
∴∠ABC=180°-∠A-∠C=155°；
又∵点B为旋转中心，E的对应点为A，
∴旋转角为∠ABE=180°-∠ABC=25°．
点评：本题考查了三角形内角和定理的运用，旋转的基本概念和性质，需要熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目
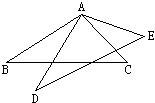15、如图，△ABC绕点A旋转后到达△ADE处，若∠BAC=120°，∠BAD=30°，则∠DAE=
10、如图，△ABC绕点C按顺时针方向旋转57°后得到△DEC，如果DC⊥BC，那么∠A+∠B等于（ ）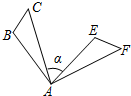
14、如图，△ABC绕点A顺时针旋转80°得到△AEF，若∠B=100°，∠F=50°，则∠α的度数是
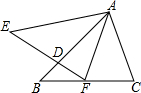（2013•永安市质检）如图，△ABC绕点A旋转至△AEF，使点C的对应点F落在BC上，给出下列结论：